九点円の定理の証明と諸性質
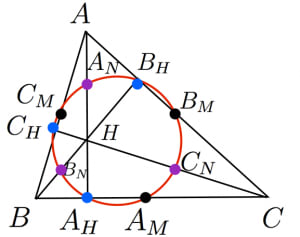
任意の三角形 において,以下の9点は同一円周上にある。
- 3辺の中点
- 垂線の足
- 垂心と各頂点の中点
九点円のことをオイラー円,フォイエルバッハ円とも言います。初等幾何好きなら知っておきたい美しい定理です。
九点円の定理の証明
九点円の定理の証明
- まずは4点 が同一円周上にあることを証明します。
- 次に, もその円周上にあることを示します。
そうすれば,対称性から残りの3点も同一円周上にあることが分かります。

-
中点連結定理より, これと, より,四角形 は長方形となり同一円周上にある。
-
上記の長方形の対角線 と はその円 の直径となる。さらに, より も の円周上にある。同様にして も の円周上にある。
以上から, は同一円周上にあることが分かったが,全く同様にして, も同一円周上にあることが分かる。しかし,三点 を通る円は1つしかないので上記の2つの円は一致する。以上から九点は同一円周上にあることが証明された。
九点円にまつわる諸性質
九点円にまつわる諸性質
- 九点円の半径は,三角形 の外接円の半径の半分です。なぜなら,九点円は「三角形 を2分の1に縮小した三角形 の外接円」だからです。
- また,内接円の半径より九点円の半径の方が明らかに大きいです。
- この2つの性質より,オイラーの不等式 が導かれます! なお,オイラーの不等式は三角関数による計算でも証明できます。→外接円の半径と内接円の半径の関係
- 九点円の中心を とおくと, は外心 と垂心 の中点となります。このことから, もオイラー線上にあることが分かります。 →オイラー線の3通りの証明
- 九点円と内接円は一点のみを共有します(内接します)。九点円と傍接円も一点のみを共有します(外接します)。これをフォイエルバッハの定理と言います。フォイエルバッハの定理は非常に美しいですが,証明はかなり難しいです。 →フォイエルバッハの定理と計算による証明
- 九点円の3次元バージョンが24点球です。→直辺四面体(垂心四面体)と24点球の定理
入試や数学オリンピックで,九点円の定理を知らないと解けないような問題は出題されないと思いますが,証明の流れを理解しておくとJMOの本選以降で役に立つかもしれません。
九点円の図を睨んで平行な直線がいっぱいイメージできれば玄人です。











