ギリシアの三大作図問題
三大作図問題とは
- 円積問題
- 立方体倍積問題
- 角の3等分問題
の3つのことである。
作図問題とは?
作図問題とは?
作図とは
- (目盛りの無い)定規で直線を引く
- コンパスで円を描く
の2つのみを用いて図形をつくることです。
作図問題は,ある図形が作図可能かという問題です。
この記事では,歴史的にも数学的にも重要な三大作図問題を紹介します。古代ギリシアから議論されていたこともあり,ギリシアの三大作図問題とも呼ばれます。
前半では,三大作図問題の準備として,作図でできること・できないことを整理します。
作図でできること
1.足し算・引き算
コンパスと定規を用いて足し算ができます。
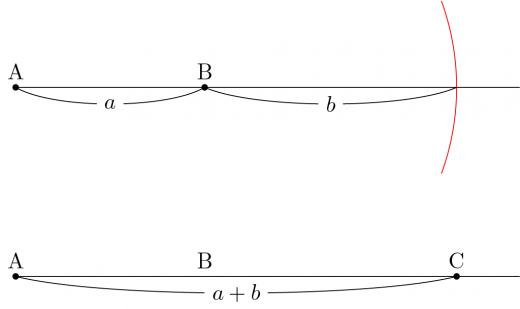
長さ の線分と長さ の線分が与えられている上で,長さが の線分を作図してみます。
- となる半直線 を引く。
- コンパスで を取る。
- を中心に半径 の円を描く。
- 円と直線の交点を とおく。
このようにすると となります。
2.掛け算・割り算
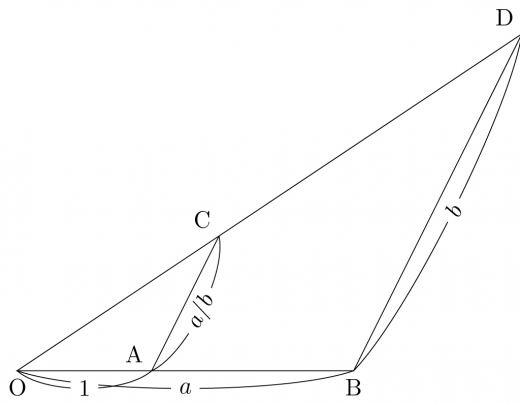
長さ の線分と長さ の線分に加えて,単位の基準となる長さ の線分が与えられている状態から, を作図してみます。
- 同一直線上に と を取る。
- を取る。
- を通り と平行な直線と, の交点を とする。
このようにすると となります。

より ∽
よって相似比 が得られ,
同様に も作図可能です。(下図)
3.平方根
平方根も作図できます。
- 直線上に3点 を, となるように取る。
- を直径とする円を描く。
- を通り, と垂直な直線を引く。
- 直線と円の交点を とする。
このようにすると となります。
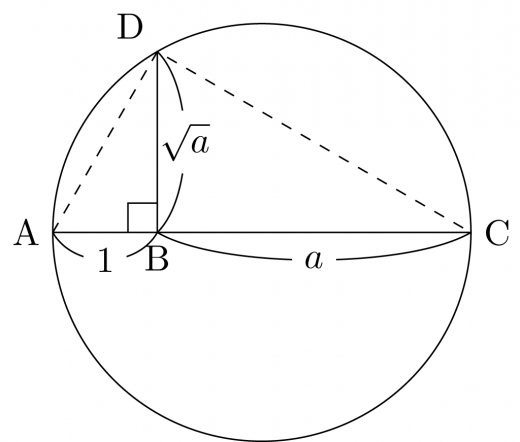
図において ∽ となることから, となり, が得られます。
平方根の長さを作図する2通りの方法 もチェックしてみてください。
作図可能数
作図可能数
長さ の線分から,作図によって得られる(正の)実数を 作図可能数 といいます。
上で見たように,(正の)整数や有理数は作図可能です。また, の出てくる数も作図可能です。
-
-
(→ このことから正五角形が作図可能であることが示されます)
作図可能性に関する定理
超越数は作図可能数ではない。
超越数とは,代数方程式の解ではない数のことです。→超越数の意味といくつかの例
実際「作図できるなら代数方程式の解になる」ことが少し頑張れば証明できます。この対偶を取ると定理1を得ます。
また,体論(ガロア理論)を用いた作図可能数に関する定理もあります(正確に述べるのが難しいため,ここでは割愛します)。
-
は超越数なので作図可能ではありません。
-
は作図可能ではありません。
-
も作図可能ではありません。
円積問題
円積問題
円積問題とは,与えられた半径の円と同じ面積の正方形を作図できるかという問題です。
半径を とすると面積は です。正方形の一辺を とすると という式が成り立ちますね。
ゆえに という長さを作図すれば良いことになります。
こうして円積問題とは, は作図可能数かという問題に置き換えられます。
円積問題は が超越数であることから,定理1を認めると作図不可能であることがわかります。
立方体倍積問題
立方体倍積問題
立方体倍積問題とは,与えられた立方体の2倍の体積を持つ立方体を作図できるかという問題です。
元々の立方体の一辺の長さを ,2倍の体積を持つ立方体の一辺の長さを とすると, という式が成り立ちます。
こうして立方体倍積問題とは, は作図可能数かという問題に置き換えられます。
定理2を認めると, は作図可能数ではありません。よって立体倍積問題は解けないことになります。
超越的な方法による作図
定規とコンパス以外の道具を使うことで, を作図することができます。
具体的には,シッソイドという曲線を活用すれば作図できます。
詳しくは シッソイド(疾走線) をご覧ください。
角の3等分問題
角の3等分問題
角の3等分問題とは,任意に与えられた角を三等分できるかという問題です。
与えられた角の大きさを としましょう。このとき 三倍角の公式 より が得られます。 とおくと, の解は作図可能数かという問題に置き換えられます。
の場合, となり作図可能です。
一方 の場合, は作図可能ではありません(この証明についてはより深くガロア理論を勉強するとわかります。今後の記事にご期待ください)。
超越的な方法による作図
定規とコンパス以外の道具を使うことで, を作図することができます。
具体的には,コンコイドという曲線を活用すれば作図できます。
詳しくは ニコメデスのコンコイド をご覧ください。
まとめ
まとめ
作図問題・作図可能数・三大作図問題について解説しました。
三大作図問題はどれも不可能という残念な結果となりましたが,この問題を元に代数学が発展したとも言えます。
また,重要な作図問題として「作図可能な正多角形はどのようなものか」も有名です。作図可能数とも深い関わりがあります。→正多角形の作図可能性の条件
square the circle(円を四角にする)で「不可能なことをする」という意味のイディオムになります。











