重心 G と外心の距離に注目すると,ライプニッツの不等式は自然に導かれます。
本質的なポイントの1つは
AG2=92b2−2c2−a2
と表されることです。→ 三角形の五心と頂点までの距離
重心の議論
中線定理より
AB2+AC2=2(AM2+BM2)
である。整理することで
AM2=2AB2+AC2−2BM2=42b2+2c2−a2
を得る。
AMAG=32 であるため
AG2=92b2+2c2−a2
である。
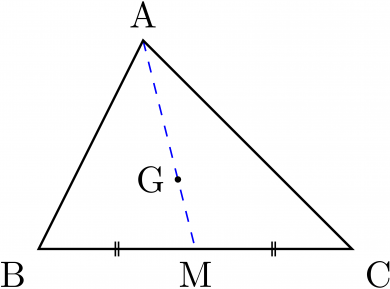
同様に BG,CG も計算できる。
重心の性質を用いる方法
次の事実が成立します。
定理
三角形 ABC とその内部の点 P について
AP2+BP2+CP2
が最小になるのは,P が三角形 ABC の重心であるときである。
つまり,三角形 ABC の重心を G とすると
AP2+BP2+CP2≧AG2+BG2+CG2
が成り立ち,P=G のとき等号が成立する。
→ 三角形の頂点からの2乗距離の和は重心で最小になる
これを用いて証明しましょう。
証明
3R2=AO2+BO2+CO2
である。
前述した事実を P=O で考えると
3R2=AO2+BO2+CO2≧AG2+BG2+CG2=92b2+2c2−a2+92c2+2a2−b2+92a2+2b2−c2=3a2+b2+c2
が成り立つ。
辺々払って
9R2≧a2+b2+c2
を得る。
OG を直接計算する方法
OG を直接計算してもよいでしょう。
方針
重心 G と外心 O の距離を頑張って求めると目標の式が登場します。その際,三角形 AOM と辺 AM の内分点 G に注目することで機械的に計算できます。→スチュワートの定理の証明とその仲間
証明
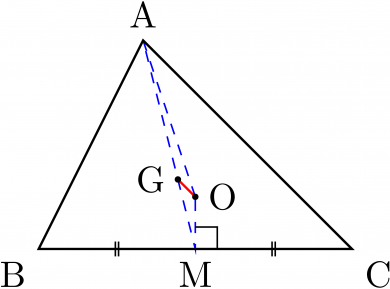
辺
BC
の中点を
M
とおくと,
- 定義より,AO=R
- 三平方の定理より,MO2=R2−4a2
- 中線定理より,AM2=42b2+2c2−a2
よって,スチュワートの定理または余弦定理を用いて
OG を求めることができる。
今回は余弦定理によって計算してみよう。まず
cos∠OAM=2OA⋅AMOA2+AM2−OM2
となる。同じく余弦定理によって
OG2=OA2+AG2−2OA⋅AGcos∠OAM=OA2+94×AM2−2OA⋅AG⋅2OA⋅AMOA2+AM2−OM2=OA2+94×AM2−32(OA2+AM2−OM2)=31OA2−92AM2+32OM2=31R2−92×42b2+2c2−a2+32(R2−4a2)=R2−91(a2+b2+c2)
を得る。ただし途中,重心の性質 AMAG=32 を用いた。
OG2=R2−9a2+b2+c2
よってライプニッツの不等式が成立する。













