ワイブル分布

概要

ワイブル分布は「製品などが故障する確率（寿命）」を表す分布として使われることが多いです。例えば，$m=2$ の場合のワイブル分布は図のようになります。

時刻 $t=t_0$ 付近で故障しやすい状況（寿命が $t=t_0$ くらいになる確率が高い状況）です。

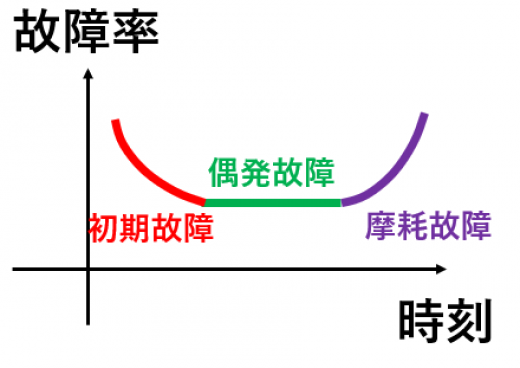
バスタブ曲線

多くの製品の故障は

1. 初期故障（時間とともに故障率が減る）
2. 偶発故障（時間がたっても故障率は変わらない）
3. 摩耗故障（時間とともに故障率が増える）

の3つに分割できます。故障率の時間変化をグラフで書いてみると，バスタブっぽいのでバスタブ曲線と言います。 実は，上記1～3はそれぞれ別のワイブル分布で表現できる場合が多いです。なぜなら，

• 「故障率が時間のべき関数 $t^{m-1}$ で表せるような製品がいつ故障するのか」はワイブル係数が $m$ であるワイブル分布で表現できます（詳細は後述）。
• 1～3はそれぞれ「故障率が時間のべき関数で表せる」で近似できる場合が多いです。例えば，1は $y=\dfrac{1}{\sqrt{t}}$ など，2は定数 $y=c$，3は2次関数 $y=t^2$ などで近似できそうです。

ワイブル係数 $m$ を変化させると分布の形状が変わります。 特に，

• $m=1$ のとき指数分布になります。確率密度関数は $f(t)=e^{-t}$ です。→指数分布の意味と具体例

• $m=2$ のときレイリー分布になります。確率密度関数は $f(t)=2te^{-t^2}$ です。→レイリー分布の期待値、分散、正規分布との関係

• $m=0.5$ のとき図のような赤い分布になります。

• ワイブル分布の基本形は， $$f(t)=mt^{m-1}\exp(-t^m)$$ でした。パラメータは $m$ です。

• 基本形に対して，$t$ 軸方向に $\tau$ 倍に拡大した $$f(t)=\dfrac{m}{\tau}\left(\dfrac{t}{\tau}\right)^{m-1}\exp\left\{-\left(\dfrac{t}{\tau}\right)^m\right\}$$ もワイブル分布です。パラメータは $m,\tau$ の2つです。

• さらに，$t$ 軸正の向きに $t_0$ だけ平行移動した $$f(t)=\dfrac{m}{\tau}\left(\dfrac{t-t_0}{\tau}\right)^{m-1}\exp\left\{-\left(\dfrac{t-t_0}{\tau}\right)^m\right\}$$ もワイブル分布です。パラメータは $m,\tau,t_0$ の3つです。

$m$ を形状パラメータ（ワイブル係数），$\tau$ を尺度パラメータ（特性寿命），$t_0$ を位置パラメータと言います。

よく使われるパラメータが2つのワイブル分布 $$f(t)=\dfrac{m}{\tau}\left(\dfrac{t}{\tau}\right)^{m-1}\exp\left\{-\left(\dfrac{t}{\tau}\right)^m\right\}$$ を考えます。

累積分布関数

累積分布関数は，以下の式で求められます。 $$F(t)=\displaystyle\int_0^tf(t)dt=1-\exp\left\{-\left(\dfrac{t}{\tau}\right)^m\right\}$$ $F(t)$ は時刻 $t$ までに故障する確率を表します。不信頼度と言うこともあります。

信頼度（故障しない確率）

$1$ から累積分布関数を引いた値： $$R(t)=1-F(t)=\exp\left\{-\left(\dfrac{t}{\tau}\right)^m\right\}$$ は時刻 $t$ までに故障しない確率を表します。信頼度と言うことがあります。

故障率

$$\dfrac{f(t)}{R(t)}=\dfrac{m}{\tau}\left(\dfrac{t}{\tau}\right)^{m-1}$$ は時刻 $t$ での故障率を表します。つまり「時刻 $t$ までに故障しないもとで，$t$ から $t+\Delta t$ の間に故障するという条件付き確率」が $\dfrac{f(t)}{R(t)}\Delta t$ になります。

つまり，ワイブル分布は故障率が $t$ のべき関数であるような分布と言えます。$m=1$ の前後で振る舞いが以下のように変わります：

• $m=1$ の場合は故障率が一定
• $m<1$ の場合は故障率が時間とともに小さくなる
• $m>1$ の場合は故障率が時間とともに大きくなる

期待値

期待値は，以下の式で求められます。 $$E=\displaystyle\int_0^{\infty}f(t)dt=\tau\Gamma\left(1+\dfrac{1}{m}\right)$$ 故障するまでにかかる時間の平均（平均故障時間，Mean Time To Failure）を表します。$\Gamma$ はガンマ関数です。→ガンマ関数（階乗の一般化）の定義と性質