コーシー分布とその期待値などについて

更新 2021/03/07

コーシー分布について解説します。

コーシー分布

確率密度関数が $f(x)=\dfrac{1}{\pi (1+x^2)}$ であるような連続型確率分布を（標準）コーシー分布と言う。

期待値が存在しない分布，裾が重い分布の代表です。

コーシー分布について

標準コーシー分布の確率密度関数のグラフは図のようになります。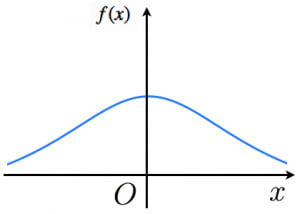正規分布と同じく左右対称な分布です。 $\dfrac{1}{\pi}$ は正規化定数です。
（ $\displaystyle\int_{-\infty}^{\infty}\dfrac{dx}{1+x^2}=\pi$ に注意）
標準コーシー分布を一次変換したもの（確率密度関数が $f(x)=\dfrac{1}{\pi\gamma\{1+(\frac{x-\mu}{\gamma})^2\}}$ である分布）を一般にコーシー分布と言います。
コーシー分布は物理ではブライト・ウィグナー分布やローレンツ分布とも呼ばれます。いろいろな名前がついていますね。

具体例

例

$\theta$ が $(0,\pi)$ の一様分布に従うとき， $\tan\theta$ は標準コーシー分布に従う。

確率変数の変換公式を用いて簡単に証明できます。練習にどうぞ！

コーシー分布の期待値

コーシー分布には期待値（平均）は存在しない。

平均はあきらかに0でしょ！って思いたくなりますが，そうではないのです。

説明

定義に従って期待値を書き下すと，

$\displaystyle\int_{-\infty}^{\infty}\dfrac{x}{1+x^2}dx$ と広義積分になる。

これは， $\displaystyle\int_a^b\dfrac{x}{1+x^2}dx=\dfrac{1}{2}\log(1+b^2)-\dfrac{1}{2}\log (1+a^2)$

について $a\to -\infty,b\to \infty$ としたもの（極限は独立に取る）であり，この極限値は存在しない。

正規分布とコーシー分布

いずれも左右対称の分布ですが，
正規分布は「外れ値を取る確率が低い（裾が軽い）」
コーシー分布は「外れ値を取る確率が高い（裾が重い）」
分布の具体例として，しばしば取り上げられます。
外れ値が重要な意味を持つような状況では，裾が重い分布を用いて議論するのか，軽い分布を用いて議論するのかの選択が重要になります。
（例えば「証券価格の大暴落が起こる確率はそこまで低くなく，正規分布のような裾の軽い分布でモデル化するのは難しい」という話を聞いたことがあります）

大数の法則が成立しない

大数の法則は期待値の存在を仮定しています。そのためコーシー分布に対しては大数の法則は成立しません。
標本平均はサンプルサイズを増やすと
000
 に近づきそうですが，外れ値を取る確率が高いためにそううまくはいかないのです。
同じく，中心極限定理も成立しません。
このように
「期待値の存在」や「大数の法則」など当たり前に成り立ちそうなことも成り立つとは限らないことの具体例として，コーシー分布は話題に挙がることが多いです。
考えてみると，コーシーと名のつく数学用語や定理は大量にありますね。
Tag:いろいろな確率分布の平均，分散，特性関数などまとめ

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！