ポアソン分布の意味と平均・分散
ポアソン分布とは「一定時間内にランダムなイベントが何回発生するか」を表す分布。
ポアソン分布について,意味・練習問題・確率関数の導出・期待値の計算方法を紹介します。
ポアソン分布とは
ポアソン分布とは
ポアソン分布は,ランダムなイベントの発生回数を表す分布です。
地震の発生回数を「ランダムなイベント」とみなすと,「これから 年間のうちに地震が発生する回数」がポアソン分布で計算できる。
※「ランダムなイベント」とは大雑把に言うと「起こる確率が常に一定である」ようなイベントのことです。
ポアソン分布の確率関数
ポアソン分布の確率関数
つまり,単位時間あたり平均 回起こるようなランダムなイベントが,単位時間に 回発生する確率は です。
例えば, の場合の確率関数は図のようになる。
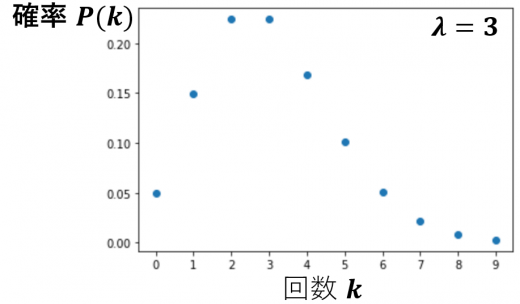 年に
平均
回起こるようなランダムなイベントが,これから
年のうちにちょうど
回起こる確率は,
年に
平均
回起こるようなランダムなイベントが,これから
年のうちにちょうど
回起こる確率は,
と計算できる。
ポアソン分布の確率の計算は,例えば WolframAlpha に(2.7182818^{-3}3^2)/2! と入力すればできます。
はネイピア数(自然対数の底)で,およそ です。世の中に登場するいろいろな確率を表すポアソン分布が を使って表せるのがおもしろいです。
練習問題:1回も発生しない確率
練習問題:1回も発生しない確率
単位時間あたり平均 回起こるようなランダムなイベントが,単位時間に 回も発生しない確率はいくらか?
, としてポアソン分布の確率関数を計算すると,
つまり,およそ %。
ただし, であることを使いました。
ポアソン分布の導出
ポアソン分布の導出
ポアソン分布を導出します。つまり,以下の定理を証明します。
単位時間あたり平均 回起こるようなランダムなイベントが,単位時間に 回発生する確率が,ポアソン分布: で表せる。
ポアソン分布を二項分布の極限としてとらえます。
以下のように考えて を求める。
- 成功確率が であるような独立な試行を 回行う。成功回数の期待値は によらず である。
- 回の試行のうち 回成功する確率は,反復試行の確率の公式より, である。
- としたものが,求める確率 となるはずである。
ここまで理解できればあとは計算するのみ。極限のよい練習問題。
上記の議論より,
ただし,最後の変形で,
を用いた。
ポアソン分布と指数分布の関係
ポアソン分布と指数分布の関係
ランダムなイベントに関する確率分布として,ポアソン分布の他に指数分布があります。比較してみましょう。
-
ポアソン分布は,ランダムなイベントの発生回数を表す分布でした。ポアソン分布の確率変数は「回数」を表すので,ポアソン分布は離散型確率分布です。
-
一方, 指数分布は,ランダムなイベントの発生間隔を表す分布です。指数分布の確率変数は「時間」を表すので,指数分布は連続型確率分布です。
参考:指数分布の意味と具体例
ポアソン分布が確率分布であることの確認
ポアソン分布が確率分布であることの確認
が確率分布であることを確認しておきます。
つまり, かつ を確認します。前者は自明なので後者を証明します。ポアソン分布の解析では指数関数のマクローリン展開が大活躍します。
上記の証明が理解できれば,ポアソン分布の平均と分散もほとんど同様な手法で導出できます。
ポアソン分布の平均と分散
ポアソン分布の平均と分散
ポアソン分布の平均は ,分散も
定義に従って計算していくのみです。さきほどと同様に,途中で指数関数のマクローリン展開を用います。
ポアソン分布の平均(期待値)は,
分散の方は計算を簡単にするために (期待値と分散に関する公式一覧の公式8)を用います。ほとんど同様にしてできるので練習問題にどうぞ!
なお,地震の発生回数は,厳密にはランダムなイベントではありません。例えば,1回地震が起こると,直後には余震が発生しやすくなります。











