平行六面体の話題(体積・分類・角度の三角不等式)
更新
各面が平行四辺形である六面体のことを平行六面体と呼ぶ。

平行六面体に関して3つの話題を紹介します。「体積」「平行六面体の分類」「角度の三角不等式」です。
平行六面体の体積
平行六面体の体積
平行六面体は「1つの頂点から出る3本の辺」を定めると1つに決まります。

この3本の辺に対応するベクトルを とおきます。
平行六面体の体積は,3本のベクトル を使って以下のように計算できます。
が張る平行六面体の体積は,
である。ベクトルの内積と外積を用いると以下のように簡潔に表せる:
また,行列式を使って
とも表せる。
「成分による式」が正しいことは以下の2つからわかる。
- 平行六面体の体積は四面体 の体積の6倍(四面体は底面積半分かつ錐体なので3分の1)
- 四面体 の体積はサラスの公式と使い方の記事末で導出したように になる。
「成分による式」と「内積と外積の形」が同じ式を表すことは,内積と外積の定義(成分表示)からわかる。
さらに「行列式の形」が同じ式を表すことは行列式の定義からわかる。
なお,内積と外積の形はスカラー三重積と呼ばれます。
特殊な平行六面体
特殊な平行六面体
平行四辺形の分類
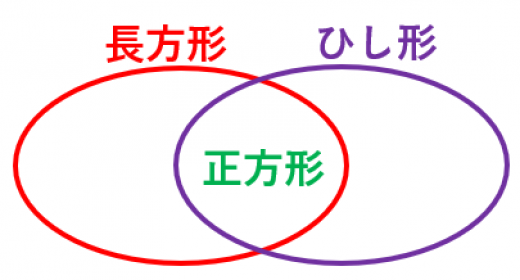 平行四辺形の中で,
平行四辺形の中で,
- 隣り合う辺が直交するものが長方形です。長方形では対角線の長さが等しいです。
- すべての辺の長さが等しいものがひし形です。ひし形では対角線が直交します。
- 長方形かつひし形なものが正方形です。
平行六面体の分類
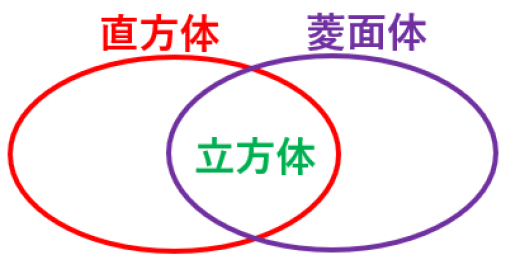 平行六面体の中で,
平行六面体の中で,
- すべての隣り合う辺が直交するものが直方体です。
- すべての辺の長さが等しいものが菱面体です。
- 直方体かつ菱面体なものが立方体です。
四面体の分類
平行六面体の8個の頂点から,隣同士を選ばないように4個を選ぶと四面体が定まります。これを「平行六面体が定める四面体」と呼ぶことにします。
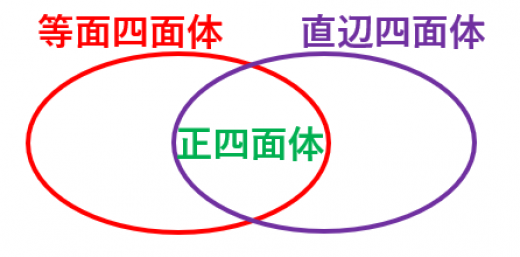 四面体の中で,
四面体の中で,
- 3組の対辺の長さがそれぞれ等しいものを等面四面体と言います。等面四面体は直方体から定まります。→等面四面体とその性質
- 3組の対辺がそれぞれ直交するものを直辺四面体と言います。直辺四面体は菱面体から定まります。→直辺四面体(垂心四面体)と24点球の定理
- 等面四面体かつ直辺四面体なものが正四面体です。正四面体は立方体から定まります。
角度の三角不等式
角度の三角不等式
任意の1次独立な3本の空間ベクトル に対して
ただし, は と がなす角。 も同様。
が張る平行六面体を考える。

に集まる角度は 未満なので
よって
※角度の三角不等式,他のおもしろい証明方法があればぜひ教えてください。
ダンボールを潰すときに「お,平行六面体」と思うことがあります。











