垂足三角形の意味と5つの性質
三角形について,各頂点から対辺におろした垂線の足がなす三角形を垂足三角形と言う。
垂足三角形のいろいろな性質を紹介します。
垂足三角形と内心
垂足三角形と内心
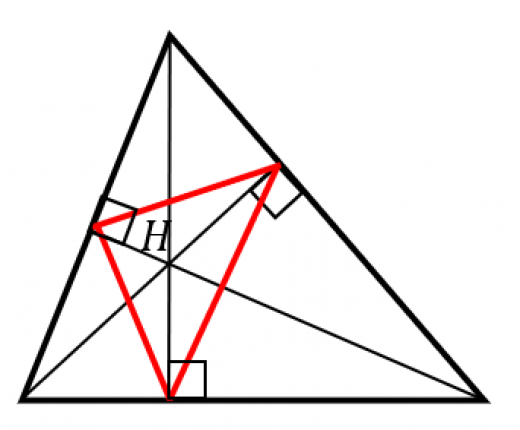
鋭角三角形の垂心 は,その垂足三角形の内心と一致する。
前提定式:3本の垂線は1点 で交わります。これを垂心と言います。→垂心の存在の3通りの証明
が の二等分線であることを証明する。

- 四角形 は直角が2つあり,円に内接する四角形である。よって円周角の定理より
- 同様に四角形 も円に内接する四角形であり,円周角の定理より
- 同様に四角形 も円に内接する四角形であり,円周角の定理より
よって,
同様に も角の二等分線である。よって, は三角形 の内心。
垂足三角形と傍心
垂足三角形と傍心
鈍角三角形の垂心は,その垂足三角形の傍心と一致する。

- 鈍角三角形の場合は垂心 は三角形 の外側です。
- 性質2の証明は性質1の証明とほぼ同様です。
- 内心と傍心は似ています。→傍心の意味と性質・内心との比較
- 図を眺めていると,4つの三角形 の垂足三角形はすべて一致することもわかります!
垂足三角形と線分和
垂足三角形と線分和
鋭角三角形 において,垂足三角形の周の長さは,
は三角形 の外接円の半径です。
三角形 と は相似であり,相似比は
よって,
 正弦定理と倍角の公式を使って変形すると,
正弦定理と倍角の公式を使って変形すると,
も同様に計算できて,周の長さは
となる。このままでもよいが,三角形の内角における和積公式を使うと上式は
となる。
性質3をふまえて,とてもおもしろい性質4を紹介します。
鋭角三角形 の各辺上を が動く。 が最小になるのは, が垂足三角形のとき。
線分和の最小値を考えるときは,折れ線にしましょう。
を に関して折り返した点を とし, に関して折り返した点を とする。

よって, を固定したとき, の最小値は の長さと等しい。
次に最適な を求める。二等辺三角形 に注目すると,
これが最小になるのは と が垂直なとき(※)。
同様に, も垂線の足であることがわかるので,最小値を達成するのは垂足三角形の場合。
(※)のうしろは,以下のような議論でもOKです:
の最小値は
となり,垂足三角形の周長と一致する。よって,垂足三角形が を最小にする(さらに,上記の議論より最小値を達成する は1つに決まるので,他の解はない)。
垂足三角形の面積
垂足三角形の面積
鋭角三角形 の面積を とすると,その垂足三角形の面積は,
周の長さには の積が出てきて,面積には の積が出てきました。証明はとてもよい練習問題です!
読み方は自信ないですが「たれあし」ではなく「すいそくさんかっけい」だと思います。











