分割数の意味と性質・ヤング図形の活躍

更新日時 2022/01/27

分割数の意味とおもしろい性質について整理しました。

数え上げの有名な話題です。ヤング図形や分割数の漸化式についても紹介します。

分割数とは

分割数の定義

正の整数 $n$ をいくつかの正の整数の和で表す方法の数を $n$ の分割数と言う。

$n$ の分割数を $p(n)$ と書くことにします。

例

$5$ をいくつかの正の整数の和で表す方法は，

の $7$ 通りなので $p(5)=7$ である。

以下では，分割数にまつわるおもしろい性質を3つ紹介します。

分割数に関する性質1

「 $k$ 個の正の整数に分割する方法の数」と「最大の数が $k$ であるようないくつかの正の整数に分割する方法の数」は等しい。

例えば，さきほどの例である $5$ の分割について， $k=3$ で確認してみます。

どちらも $2$ 通りで一致しますね。ヤング図形というものを使って性質1を証明してみます。

ヤング図形とは

正の整数 $n$ の分割に対して，正方形を $n$ 個並べた下図のような図形をヤング図形といいます。下図は $7=4+2+1$ という分割に対応しています。下の行に行くに連れて正方形の数が減少していきます。

ヤング図形

また，正方形の代わりに点で表したものをフェラーズ図形といいます。どちらも同じですが，正方形の中に数字を書き込んだりできるのでヤング図形の方が便利なことがあります。

ヤング図形を使えば上記の性質1を簡単に証明できます。「対応付け（全単射）をつくる」という重要なテクニックを使います。

性質1の証明

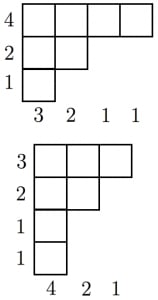
自然数分割の性質の証明

「 $k$ 個の分割」を一つとってきて，それに対応するヤング図形を書く。これを行ではなく列に関して見ると，「最大の数が $k$ である分割」に対応している（上側の図）。
逆に，「最大の数が $k$ である分割」をとってきて，そのヤング図形を列に関してみると「 $k$ 個の分割」に対応している（下側の図）。
これらの操作は互いに逆の操作になっていて，一対一対応が得られる（例えば， $4+2+1$ と $3+2+1+1$ は対応している）。

よって，両者の分割の方法の数は等しい。

2つめの性質は，分割数に関する漸化式です。

$n$ を $k$ 個の正の整数に分割する方法の数を $p_k(n)$ と書くことにします。

分割数の漸化式

$p_k(n)=p_k(n-k)+p_{k-1}(n-1)$

ただし， $k>n-k$ のとき $p_k(n-k)=0$ とします。

漸化式の証明

$n$ を $k$ 個に分割する方法について「 $1$ を含まないもの」と「 $1$ を含むもの」にわけて考える。

$1$ を含まないものは $p_k(n-k)$ 通り
なぜなら「 $1$ を含まない $n$ の $k$ 個の分割」と「 $n-k$ の $k$ 個の分割」には1対1対応があるから。実際，前者についてそれぞれから $1$ を引くと後者が得られ，後者についてそれぞれに $1$ を足すと前者が得られる。それらの操作は互いに逆の操作になっている。
$1$ を含むものは $p_{k-1}(n-1)$ 通り
なぜなら「 $1$ を含む $n$ の $k$ 個の分割」と「 $n-1$ の $k-1$ 個の分割」には1対1対応があるから。実際，前者について $1$ を一つ除くと後者が得られ，後者について $1$ を一つ加えると前者が得られる。それらの操作は互いに逆の操作になっている。