メネラウスの定理の覚え方と拡張
更新
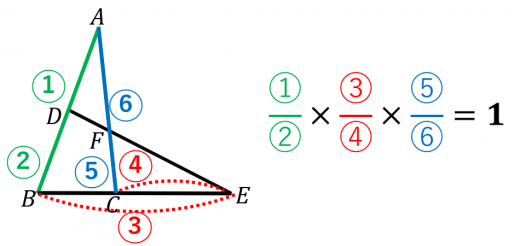
図において, が成立する。これをメネラウスの定理と言う。
メネラウスの定理は高校入試・大学入試で活躍する重要な公式です。メネラウスの定理について,2通りの覚え方(見方)と定理の拡張について解説します。
メネラウスの定理の例題
メネラウスの定理の例題
図において,, であるとき, を求めよ。
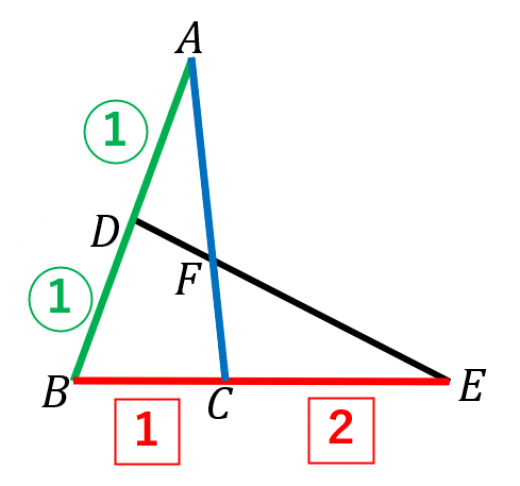
メネラウスの定理より,
ここで,問題文より , なので,
よって,
メネラウスの定理の覚え方
メネラウスの定理の覚え方

図を見ながら,以下の2つを覚えましょう。
-
メネラウスの定理は「キツネの形」に使える定理です(わかりやすさのために,図にはキツネの目を書きました)。
-
赤い矢印と青い矢印を順々に進んで比を取っていきます。 からはじめると, になります。 からはじめてなどとおぼえましょう。私はと習いました。
-
分子/分母 という主張なので,分母と分子をひっくり返してもOKです。分数を並べ替えてもOKです。つまり,六本の線分はどこからはじめても,逆順に覚えてもOKです。
と覚えても,
と覚えても(他にもいろいろある)よいということです。そのため,本によってメネラウスの定理の主張が微妙に異なって見えることがありますが,全て同値です。自分が理解しやすい形で覚えて下さい。 -
なお,キツネの図形に対しては異なるもう一つのメネラウスの定理の適用方法があります( ではなく を通る):
メリット:複雑な図形の中でキツネの図形は比較的見つけやすい。
デメリット:この覚え方だと,後述のようにメネラウスの定理を自然に拡張できない。
メネラウスの定理の別のとらえ方
メネラウスの定理の別のとらえ方

-
メネラウスの定理は「三角形と直線からなる図形に対して成立する定理」とも認識できます。
-
「適当なとこからスタートして同一直線上にある赤い点(三角形の頂点)と青い点(直線上の点)を交互に巡って比を取っていく」と覚えればOKです。また,さきほどと同様にどこからスタートしてもOKです。
メリット:メネラウスの定理を自然に拡張できる(後述)。
デメリット:複雑な図形の中で適用するのに訓練が必要。
というわけでメリットデメリットがあるので,どちらのとらえ方も知っておくとよいでしょう。
メネラウスの定理の拡張
メネラウスの定理の拡張
メネラウスの定理の「別のとらえ方」において,直線が三角形と交わらない場合でもメネラウスの定理がそのまま成立します!
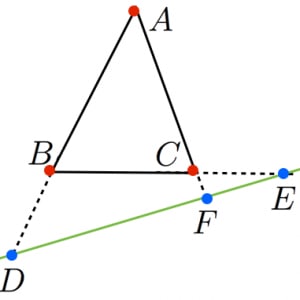
これはキツネの覚え方からでは拡張できない結果です。高校範囲ではあまり知られていないですが,難しい定理の証明などにときどき使います。
また,この場合もメネラウスの定理の逆が同様に成立します。順定理,逆定理いずれも拡張前のメネラウスの定理と同様に証明できます。
証明
証明
補助線を一本引くだけで拡張まで含めて同時に証明できます。
直線 上の点 を,直線 が直線 と平行になるようにとる。

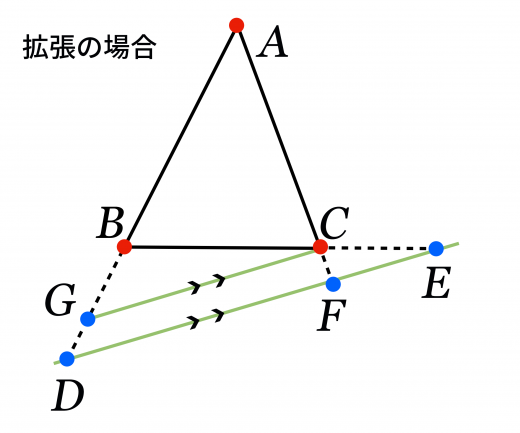
すると図より三角形 と は相似で,三角形 と も相似である。よって が成り立つ。これを代入すれば となる。
余談
余談
メネラウスの定理は「三角形」と「直線」について成立する定理でした。実は,これを三次元バージョンにして「四面体」と「平面」について成立する似たような定理もあります。
また,メネラウスの定理の難しめの応用例を以下で紹介しています。 →デザルグの定理とその三通りの証明
メネラウスの定理はチェバとくらべて一見覚えにくいですが見方によってはけっこう美しいです。











