調和点列の様々な定義と具体例

更新 2021/03/07

調和点列

同一直線上に四点 $A,\:P,\:B,\:Q$ がこの順にあるとき，

1： $AP:PB=AQ:QB$ (線分 $AB$ を同じ比で内分する点 $P$ と外分する点 $Q$ )

ならば四点 $A,\:P,\:B,\:Q$ を調和点列と言う。

調和点列の考え方は知っていると数オリでしばしば役立ちます。調和点列を使いこなすための基本的な知識を整理しました。

調和点列の同値な定義

調和点列には同値な言い換えがたくさんあります。以下の条件は全て $A,\:P,\:B,\:Q$ が調和点列であるための必要十分条件です。

2： $\dfrac{AP\times BQ}{BP\times AQ}=1$ （複比が $1$ ）

3： $PA:PB=QA:QB$ (線分 $PQ$ を同じ比で内分する点 $B$ と外分する点 $A$ )

これらが条件1と同値であることは自明ですが，場面に応じて都合がよいものを使いましょう。

4： $\dfrac{2}{AB}=\dfrac{1}{AP}+\dfrac{1}{AQ}$

5： $PQ$ の中点を $M$ とすると $AM\times AB=AP\times AQ$

4は $AP,\:AB,\:AQ$ が調和数列（逆数が等差数列）であることを表しています。調和点列と呼ばれるゆえんです。

5は調和点列であることの証明にときどき使えます。

4と5を証明しておきます。

$AP=p,\:AB=b,\:AQ=q$ とおくと，調和点列である条件は，2より， $p(q-b)=q(b-p)$ であり，これを変形すると $\dfrac{2}{b}=\dfrac{1}{p}+\dfrac{1}{q}$ となることから4が証明されます。

また， $\left(\dfrac{p+q}{2}\right)b=pq$ とも変形できることから5が導かれます。

6： $AB$ を直径とする円に関する反転で $P$ は $Q$ にうつり $Q$ は $P$ にうつる。

調和点列は反転と非常に相性がよいです（反転を知らない人はスルーしてください）。

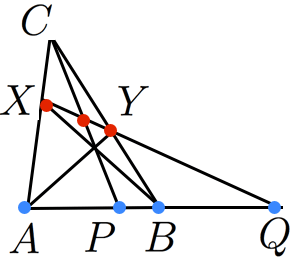
調和点列の具体例

三角形と直線を組み合わせた図のような構図には調和点列が潜んでいます。

主張1： $A,\:P,\:B,\:Q$ は調和点列

主張2： $Q$ と赤い三点も調和点列

証明

チェバの定理とメネラウスの定理を組み合わせると簡単に証明できる。

チェバの定理より，

$\dfrac{CX}{XA}\dfrac{AP}{PB}\dfrac{BY}{YC}=1$

メネラウスの定理より，

$\dfrac{CX}{XA}\dfrac{AQ}{QB}\dfrac{BY}{YC}=1$

以上二式を辺々割り算すると， $\dfrac{AP\times BQ}{BP\times AQ}=1$ となり主張1を得る。

また，この結果と複比の不変定理→複比の定義と複比が不変であることの証明より主張2が証明される。

調和点列と極線

点 $A$ を通り円 $C$ と二点 $P,Q$ で交わるような直線と $A$ に関する $C$ の極線が $B$ で交わっている。このとき， $A,\:P,\:B,\:Q$ は調和点列。

証明は，極線の方程式の証明と応用を参照して下さい。

三角形 $ABC$ の辺 $BC$ 上に四点 $X,\:P,\:Y,\:Q$ を以下のように取るとこれらは調和点列。

$X$ ： $A$ から下ろした垂線の足

$Y$ ： $\angle A$ の二等分線との交点

$P$ ：内接円との接点

$Q$ ： $A$ と反対側にある傍接円との接点

簡単な計算で証明できます。よい練習問題にどうぞ。

調和点列は意外といろいろなところに潜んでいます。

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！