根軸の性質と根心の存在定理

更新日時 2021/03/07

根心の存在定理
3つの円が互いに2点で交わるとき，3本の根軸は一点で交わる。
2つの円が2点で交わるとき，その2点を結んだ線を根軸(radical axis)と言います。
3本の根軸が1点で交わるというのはおもしろいです！
このページでは，根心の存在定理を3段階に分けて証明します。
方べきの値について
根軸について
根心の存在定理の証明
1と2は証明の道具（前提知識）の説明ですが，根軸の存在定理の証明以外にも応用される有名な話題です（例えば，国際数学オリンピック2000年の第一問は根軸の知識がないと厳しい）。

1. 方べきの値について
1. 根軸について
1. 根心の存在定理の証明

1. 方べきの値について円 OOO とその外点 AAA が与えられたとき，以下のように方べきの値 P(O,A)P(O,A)P(O,A) を定義する：
円
OOO
 と点
AAA
 を通る直線
lll
 が2つの交点を持つときその交点を
X,YX,YX,Y
 として，
P(O,A)=AX⋅AYP(O,A)=AX\cdot AYP(O,A)=AX⋅AY
 とする。
方べきの値が直線
lll
 の選び方によらず，円
OOO
 と点
AAA
 だけで決まるのがポイントです（なぜなら，方べきの定理より
AX⋅AY=AX′⋅AY′AX\cdot AY=AX'\cdot AY'AX⋅AY=AX′⋅AY′ だからです）。
よって，直線
lll
 が円
OOO
 の中心を通る場合を考えれば方べきの値は計算できます：
P(O,A)=(OA−r)(OA+r)=OA2−r2⋯(1)P(O,A)=(OA-r)(OA+r)=OA^2-r^2\cdots (1)P(O,A)=(OA−r)(OA+r)=OA2−r2⋯(1)
ただし，円の半径を
rrr
 とおきました。
ちなみに
AAA
 が
OOO
 の内部にあるときは
P(O,A)=−AX⋅AYP(O,A)=-AX\cdot AYP(O,A)=−AX⋅AY
 と定義します（定義にマイナスをつけることで方べきの値が(1)と一致して嬉しい）。

2. 根軸について

定理1

円 $O_1$ と円 $O_2$ が与えられたとき，

点 $A$ が根軸上にある⇔ $P(O_1,A)=P(O_2,A)$

「2つの円に対する方べきの値が等しい点の集合が根軸である」という主張です。

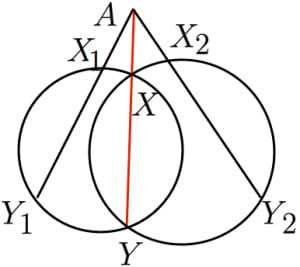
根軸の性質

根軸上なら方べきの値は等しい，の証明

$A$ が根軸上にあるとき，方べきの定理より，

$AX_1\cdot AY_1=AX\cdot AY=AX_2\cdot AY_2$

となり方べきの値は等しい。

逆の証明は少し難しいです。

方べきの値が等しいなら根軸上，の証明：

点 $A$ における方べきの値が等しいとき，

$O_1A^2-r_1^2=O_2A^2-r_2^2$

つまり $O_1A^2-O_2A^2=c$ （定数）

ここで，2点からの距離の二乗の差が等しい点の軌跡は直線になることが簡単な計算で分かるので，方べきの値が等しい点は一本の直線に乗っている。

ところが，さきほどの議論によりその直線は根軸であることが分かる。

「軌跡は一本の直線」＋「根軸上の点は条件を満たしている」→「根軸以外の点はありえない」というロジックです。

なお，二つの円が二点で交わらない場合も，根軸を「方べきの値が等しい点の集合」として定義できます。

3. 根心の存在定理の証明

いよいよ根心の存在定理の証明です！外心の存在や内心の存在を示したときと同じ感じです。

円 $O_1,O_2$ の根軸を $l_{12}$ ，円 $O_2,O_3$ の根軸を $l_{23}$ ，円 $O_3,O_1$ の根軸を $l_{31}$ とおきます。

$l_{12}$ と $l_{23}$ の交点 $A$ が $l_{31}$ 上にあることを示せばよいです。

証明

$A$ は $l_{12}$ 上の点なので定理1より

$P(O_1,A)=P(O_2,A)$ ，

同様に $A$ は $l_{23}$ 上の点なので定理1より

$P(O_2,A)=P(O_3,A)$ ，

よって， $P(O_1,A)=P(O_3,A)$

ここで，再び定理1より，点 $A$ は $O_1$ と $O_3$ の根軸 $l_{31}$ 上にあることが分かる。

根軸の存在定理は単純ですが自明ではない美しい定理です！　ブリアンションの定理の証明でも活躍します！

この記事の編集者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！