胡蝶定理(butterfly theorem)
更新
図において, は弦 の中点とする。
このとき, となる。
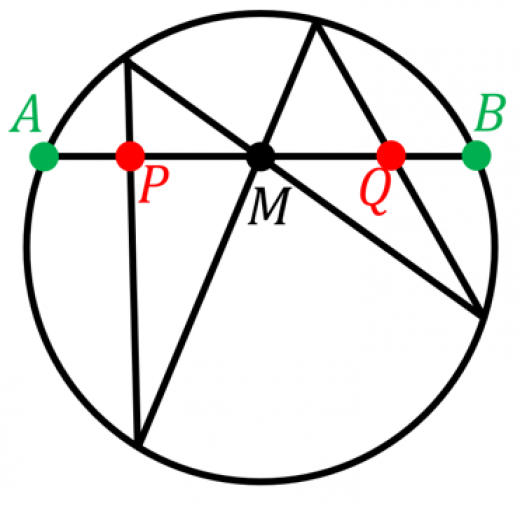
胡蝶定理の証明を2つ紹介します。
- 面積比に着目した証明
- 面積比に着目した証明
とてもおもしろい証明です。
4つの三角形の面積比に着目することで証明できます。
2つの三角形について,1組の角の大きさが等しいとき,面積比はその角をはさむ辺の積の比と等しくなります(→三角形の面積比にまつわる公式たちの公式2)。
これを4回使うことで証明できます。
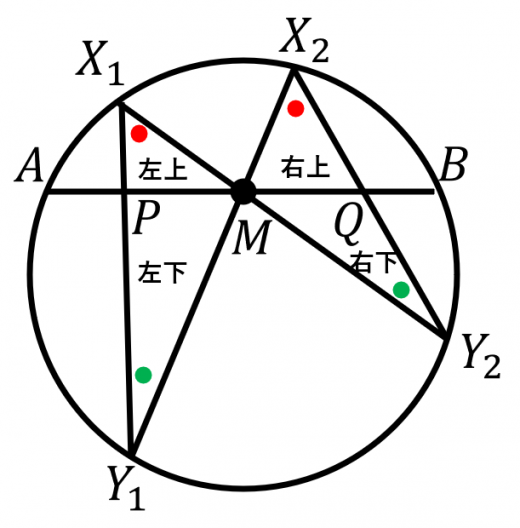 4つの三角形の面積比について,
4つの三角形の面積比について,
4つの式をすべてかけあわせると, あとは, 以外の余分なものの形を見て,方べきの定理を使うと, 以上3つの式より, つまり, なら
胡蝶定理の逆( なら )も示せました。
- 正弦定理による証明
- 正弦定理による証明
本質的には証明1とほぼ同じですが,面積比よりも正弦定理を使ったほうがわかりやすいかもしれません。
とおく。
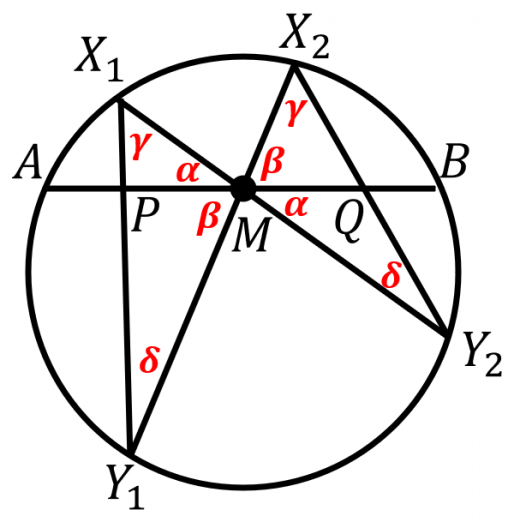
(証明1の後半と全く同じだが)方べきの定理より, あとは,これらの左辺に登場する4つの辺の長さを,正弦定理で角度の情報(および )で表す。
以上より, よって,
他にも証明方法はありますが,補助線を引く必要がないわかりやすい方法を紹介しました。











