円周角の定理とその逆の証明

更新 2021/08/22

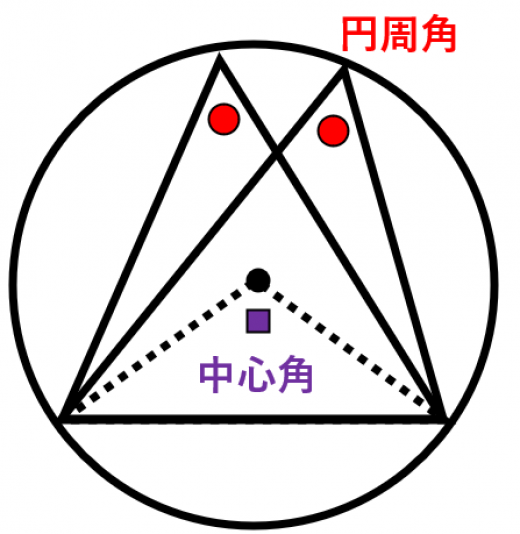
円周角の定理

円周角の定理

円周角の定理は，中学で習い高校でもよく使う重要な定理です。

この記事では，円周角の定理とその逆について意味と証明を紹介します。

円周角の定理の証明

「円周角の定理1：中心角＝円周角の2倍」を証明します。

つまり，円周角を $\angle ACB$ ，円の中心を $O$ として， $\angle AOB=2\angle ACB$ を証明します。

証明

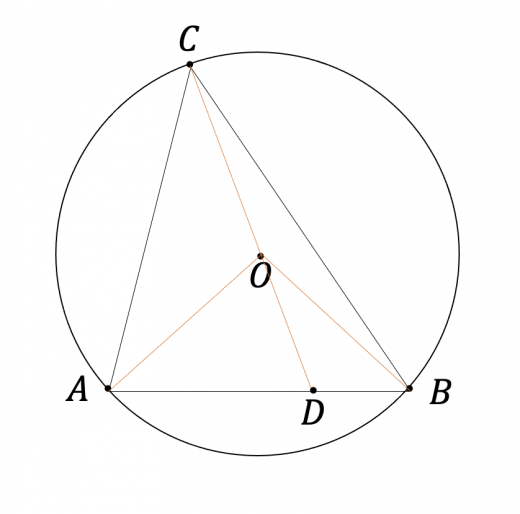三角形 $ABC$ の内側に $O$ があるとき図のように補助線を引くと，二等辺三角形より $\angle ACO = \angle CAO,\:\angle BCO = \angle CBO$ である。よって，三角形の外角より $\angle AOD = 2\ \angle ACO\\ \angle BOD = 2\ \angle BCO$ となる。以上から， $\begin{aligned}&\angle AOB\\ &=\angle AOD+\angle BOD\\ &=2\angle ACO+2\angle BCO\\ &=2(\angle ACO+\angle BCO)\\ &=2\angle ACB \end{aligned}$
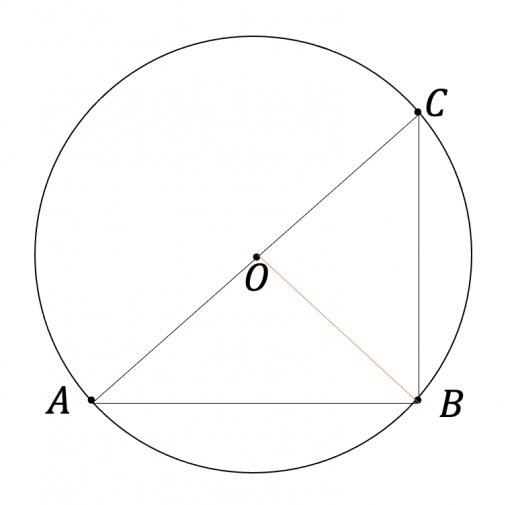三角形 $ABC$ の辺上に $O$ がある場合図のように補助線を引くと，二等辺三角形より $\angle ACB = \angle CBO$ となる。よって，三角形の外角より $\angle AOB = 2\ \angle ACB$
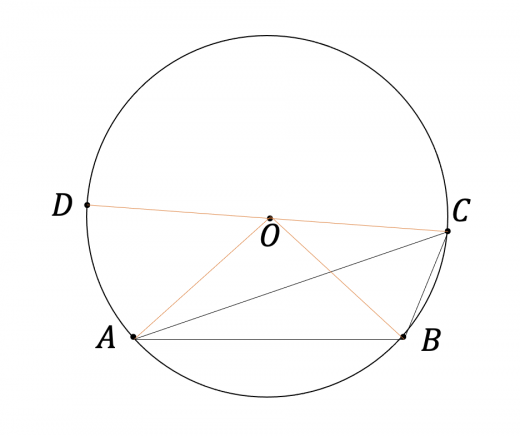三角形 $ABC$ の外側に $O$ があるとき図のように補助線を引くと，二等辺三角形より $\angle ACO = \angle CAO,\:\angle BCO = \angle CBO$ となる。よって三角形の外角より， $\angle AOD = 2\ \angle ACO\\ \angle BOD = 2\ \angle BCO$ となる。以上から， $\begin{aligned} &\angle AOB\\ &=\angle BOD-\angle AOD\\ &=2\angle BCO-2\angle ACO\\ &=2(\angle BCO-\angle ACO)\\ &=2\angle ACB \end{aligned}$

「円周角の定理2：同じ弧に対する円周角は等しい」を証明します。

円周角の定理1を用いれば簡単です。

証明

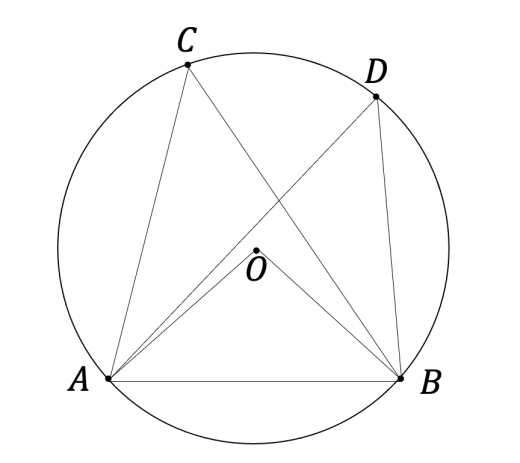
円周角の定理の証明2

「円周角の定理1：円周角＝中心角の半分」より $\angle ACB = \dfrac{1}{2}\angle AOB\\ \angle ADB = \dfrac{1}{2}\angle AOB$ よって， $\angle ACB =\angle ADB$

円周角の定理は「(円ならば)円周角は等しい」と解釈できます。実は，その逆「円周角が等しいならば円」も成立します。もう少しきちんというと，

円周角の定理の逆

4点 $A,B,C,D$ について，2点 $C,D$ が直線 $AB$ について同じ側にあり， $\angle ACB = \angle ADB$ であるならば，4点 $A,B,C,D$ は同一円周上にある。

証明

$\triangle ABC$ の外接円について考える。

もし， $D$ が円の内部にあるなら，図より $\angle ADB=\angle AEB+\angle EBD>\angle AEB =\angle ACB$ つまり， $\angle ACB \lt \angle ADB$ となる。
もし， $D$ が円の外部にあるなら，同様に $\angle ACB \gt \angle ADB$ となる。

いずれの場合も， $\angle ACB = \angle ADB$ という仮定に矛盾。よって， $D$ は円周上にある。つまり4点 $A,B,C,D$ は同一円周上にある。

円周角の定理は，より難しいいろいろな定理の証明に使われます。例えば，

タレスの定理：円に内接する三角形のうち，斜辺の長さが円の直径と等しい三角形は直角三角形となります。これはタレスの定理と呼ばれています。詳細は→直角三角形の定義とさまざまな公式
円に内接する四角形の性質：→円に内接する四角形の性質とその証明まとめ

円周角の定理自体は知っていても，3つに場合分けしてきちんと証明できる人は意外と少ないのではないでしょうか。