円に外接する四角形とその性質
円に外接する四角形とは「4つの辺すべてが同じ円に接する」四角形です。
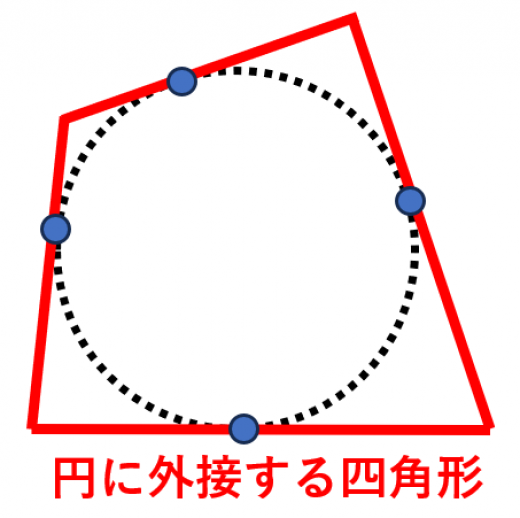
円に外接する四角形についての性質を整理しました。
円に外接する四角形と接線の長さ
円に外接する四角形と接線の長さ
まずは,円に外接する四角形の性質というより,円と接線に関する一般的な性質です。
頂点から2つの接点までの距離は等しい。つまり,

円外の点 から引いた2本の接線の接点を とするとき を示せばよい。

円の中心を とする。
- 円の半径より
- 接線より
- は共通の辺
よって,直角三角形で斜辺と他の1辺が等しいので三角形 と は合同。よって
円に外接する四角形と対辺の長さの和
円に外接する四角形と対辺の長さの和
次は最も重要な性質です。入試でも頻出です。
円に外接する四角形 について, が成立する。
導出方法も重要なので覚えておきましょう。
図のように つの接点を とおく。

点 から円に引いた二本の接線の長さは等しい(定理1)ので,
以上 つの式を足し合わせると,
よって,
四角形が円に外接する条件
四角形が円に外接する条件
実は定理1の逆も成立します。
凸な(へこんでいない)四角形 が を満たせば,その四角形はある円に外接する。
-
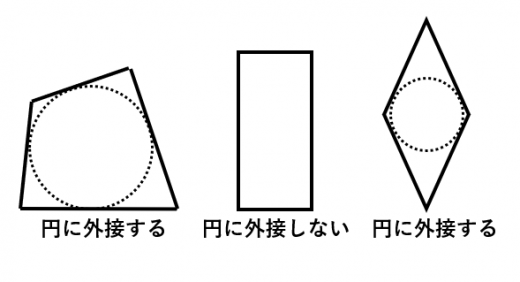
例えば,(正方形でない)長方形は上式を満たさないので「円に外接する四角形」ではありません。
-
一方,ひし型は上式を満たすので「円に外接する四角形」です。
円に外接する四角形の面積
円に外接する四角形の面積
円に外接する四角形 について,面積は
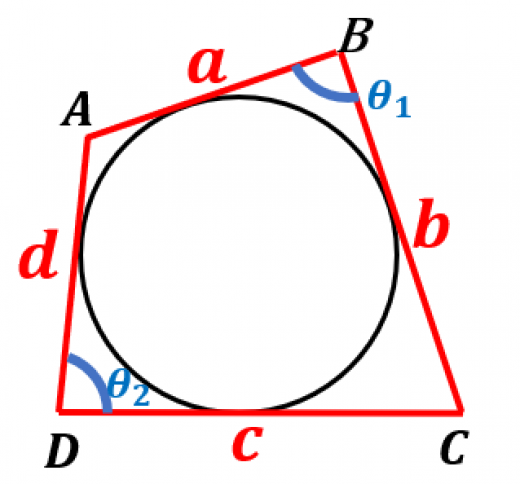
こちらは観賞用の公式です。おもしろいですが,知っていて役立つことはほとんどないでしょう。
証明にはブラーマグプタの公式の一般形であるブレートシュナイダーの公式を使います。
まず,ブレートシュナイダーの公式に現れる を計算する:
ただし,変形の途中で定理2()を用いた。
同様に, より,
よってブレートシュナイダーの公式より,四角形の面積は,
円に外接し内接もする四角形
円に外接し内接もする四角形

面積公式(定理4)が使いにくいのは,ブレートシュナイダーの公式が使いにくい理由と同じく の値を求めるのが難しいからです。
が簡単に求まる場合には威力を発揮します。
例えば,円に外接する四角形がさらに別の円に内接する場合,円に内接する四角形の性質より なので となります。
これは覚えるに値する非常に美しい公式ですね!
円に内接して別の円に外接する四角形を描くのに大変苦労しました。











