【解答・解説】東大理系数学2024
※以下の解答と解説は東京大学が公表したものではなく,当サイトオリジナルのものです。問題は東京大学第2次試験問題からの引用です。
この記事では,東京大学の2024年度入学試験の理系数学について解説します。
大問分析
| 問題番号 | 分野 | 難易度 |
|---|---|---|
| 1 | 領域 | 標準 |
| 2 | 微分積分 | 標準 |
| 3 | 確率 | 標準 |
| 4 | 図形と方程式 | 標準 |
| 5 | 体積 | やや難 |
| 6 | 整数 | 難 |
時間がかかる問題が多い印象です。特に第三問と第四問は難易度こそ高くはないものの記述が非常にヘヴィーだったのではないでしょうか。
第五問の体積はセオリー通り立体を平面で切って解きたいですが,断面の挙動が変わるタイミングを見逃しにくいです。
第六問は難問です。(2) まで完答できた人は少なかったのではないでしょうか。
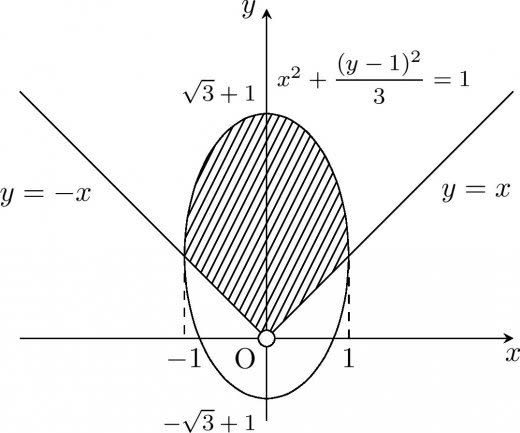
第一問 [領域]
第一問 [領域]
座標空間内の点 をとる。 平面上の点 が次の条件 (i),(ii),(iii) をすべて満たすとする。
がとりうる範囲を 平面上に図示せよ。
とおく。
条件 (ii) より また より である。これより となる。また,変形すると となる。二乗すると より , を得る。
条件 (iii) より である。
と上の2つの不等式を合わせると,
となる。整理すると
それぞれ二乗して整理すると となる。1つ目の
よって
第二問 [微分積分]
第二問 [微分積分]
次の関数 を考える。
- を満たす実数 で, となるものを求めよ。
- 1 で求めた に対し, の値を求めよ。
- 関数 の区間 における最大値と最小値を求めよ。必要ならば, であることを用いてよい。
第二問は三角関数と微積分の問題でした。早速積分の形で表された関数の微分からスタートです。
であるため となる。ここで を満たす実数で とおくと, より であるため, となるのは のときである。
を計算する問題です。ここはサクッと済ませたい。
より は の解である。
方程式を解くと が解である。 より である。
(3) も難しいことはないです。計算ミスに注意したいところ。
以下 とする。
増減表を書くと となる。
よって最小値は である。
最大値は か のいずれか。
となる。
で より であるため である。
こうして最大値は である。
第三問 [確率]
第三問 [確率]
座標平面上を次の規則 (A),(B) に従って 1 秒ごとに動く点 P を考える。
(A) 最初に,P は点 にいる。
(B) ある時刻で P が点 にいるとき,その 1 秒後には P は
-
確率 で 軸に関して と対称な点
-
確率 で 軸に関して と対称な点
-
確率 で直線 に関して と対称な点
-
確率 で直線 に関して と対称な点
にいる。以下の問いに答えよ。ただし,(1) については,結論のみ書けばよい。
-
P がとりうる点の座標をすべて求めよ。
-
を正の整数とする。最初から 秒後に P が点 にいる確率と,最初から 秒後に P が点 にいる確率は等しいことを示せ。
-
を正の整数とする。最初から 秒後に P が点 にいる確率を求めよ。
(1) は何回か実験すれば分かるでしょう。答案は結論だけでいいのですが,今回はキチンと論証をしてみましょう。
以下,(B) の規則の操作を上から1~4ということにする。
各操作を行うと点 は次の点に映る。
※ 1,2は簡単である。3,4については映った先の点と との中点が ()上にあることを踏まえるとすぐに分かる。
よって,各操作は,符号を入れ替る操作と座標を入れ替える操作の合併である。
こうして ,(複合任意)と分かる。
実験をすると偶数秒後と奇数秒後で行きうる点が異なることに気付けるでしょう。これを元に帰納法で示します。
点 は,奇数秒後には のどれかに,偶数秒後には のどれかにあることが帰納的に示すことができる。
以下 秒後について, についての帰納法により証明すればよい。
のとき
-
にある確率:同じ操作を2回行う確率であるため
-
にある確率:操作1と操作2を行うときと操作3と操作4を行うときの2パターンがあるので
こうして確率は等しいことが分かる。
のとき成立すると仮定する。
2回の操作で がそれぞれ に移る確率を調べる。
-
に移る確率
- :同じ操作を2回連続で行うときであるため
- :操作1と操作2を行うとき,もしくは操作3と操作4を行うときであるため
- :操作1と操作3を行うとき,もしくは操作2と操作4を行うときであるため
- :操作1と操作4を行うとき,もしくは操作2と操作3を行うときであるため
-
に移る確率
- :操作1と操作2を行うとき,もしくは操作3と操作4を行うときであるため
- :操作1と操作2を行うとき,もしくは操作3と操作4を行うときであるため
- :操作1と操作4を行うとき,もしくは操作2と操作3を行うときであるため
- :操作1と操作3を行うとき,もしくは操作2と操作4を行うときであるため
こうして を得る。
※ ただし で 秒後に が にある確率を表した。
こうして のときも従うため,任意の に対して命題は従う。
(2) を元に漸化式を立てましょう。
秒後に点 P が
- にある確率を
- にある確率を
- にある確率を
- にある確率を
とおく。
が偶数のとき,P は のいずれかにあるため, である。同じく が奇数のとき,
以下 とおきなおして計算する。
秒後に にあるのは
- 秒後に にある上で,軸に関する対称移動2回行った場合
- 秒後に にある上で,直線 に関する対称移動2回行った場合
- 秒後に にある上で,軸に関する対称移動を1回,直線 に関する対称移動1回行った場合
である。よって漸化式として を得る。整理すると である。変形して で に注意してこれを解くと, のとき を得る。
よって求める確率は
第四問 [図形と方程式]
第四問 [図形と方程式]
とおく。 を満たす実数 に対し,座標平面上の点 を通り,この点において放物線 と共通の接線を持ち, 軸上に中心を持つ円を とする。
- 円 の中心の座標を ,半径を とおく. と を の整式で表せ。
- 実数 は を満たすとする。円 が点 を通るような実数 は の範囲にいくつあるか。
第四問は図形と方程式の問題です。ハードな計算が必要です。
での放物線の接線は の接線でもあるため, での放物線の法線は の中心を通る。
より法線の式は である。
円の中心の座標 を代入すると となるため である。
円の方程式は である。 を代入することで
(1) さえ解けてしまえば (2) はただ計算するだけです。
円 が を通るので となる。整理すると である。ここで とおくと, と の交点の数を考えればよい。
より増減表は となる。
の取る値を計算する。
よってグラフは次のようになる。
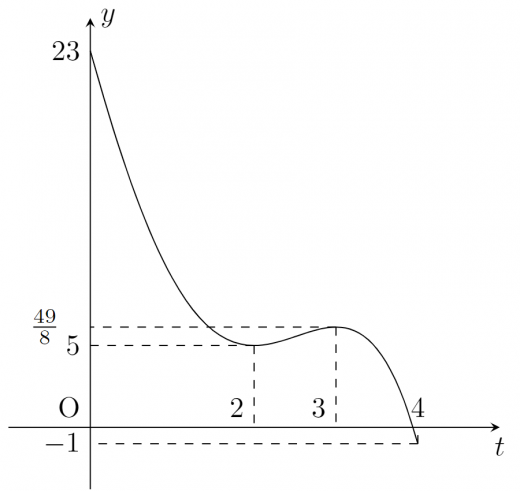
より のとり得る範囲は である。
こうして
第五問 [体積]
第五問 [体積]
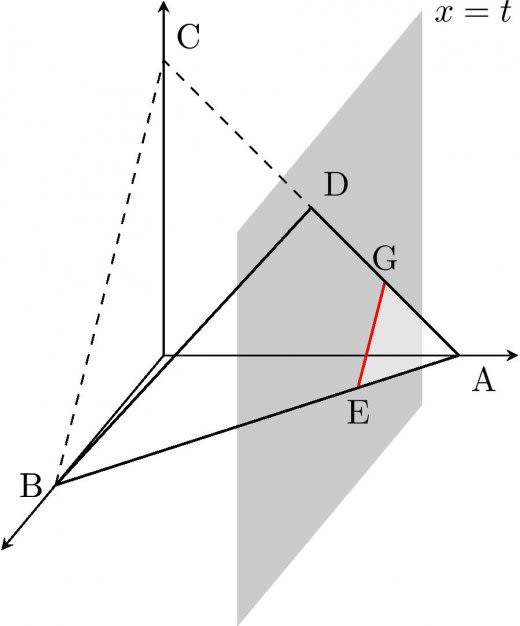
座標空間内に3点 ,, をとり, を線分 の中点とする。三角形 の周および内部を 軸まわりに1回転させて得られる立体の体積を求めよ。
第五問は平面図形を回転した立体の体積を求める問題でした。セオリー通り適切な平面で切った断面を考えていきます。
平面 と三角形 の交わりを調べる。
は と を結ぶ線分であるため,かならず平面 と交わる。
平面 と辺 の交点を とおく。 であるため を得る。
一方, の 座標は であるため,三角形 のどの辺と平面 が交わるか場合分けが生じる。
まずは の範囲で調べましょう。
- のとき
平面 と辺 の交点を とおく。 であるため, を得る。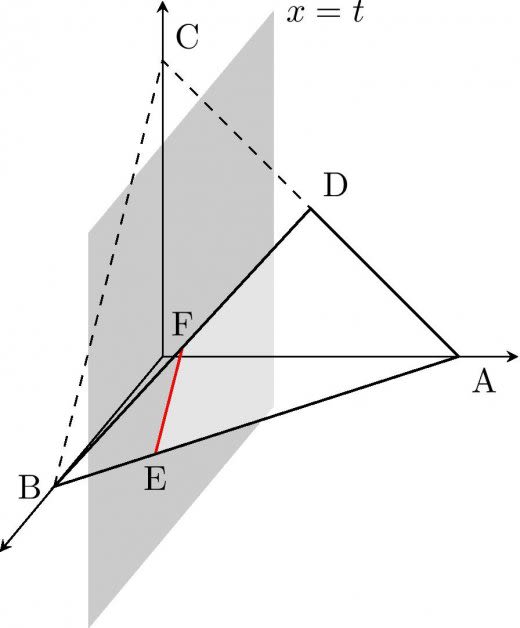 , はともに直線 上にある。
, はともに直線 上にある。
上図より の 座標が より大きいか小さいかで, 軸と最も近い直線 上の点が異なる。
不等式 を解くと を得るため,これを境に場合分けをする。
-
のとき
- 軸から最も近い点:
- 軸から最も遠い点:
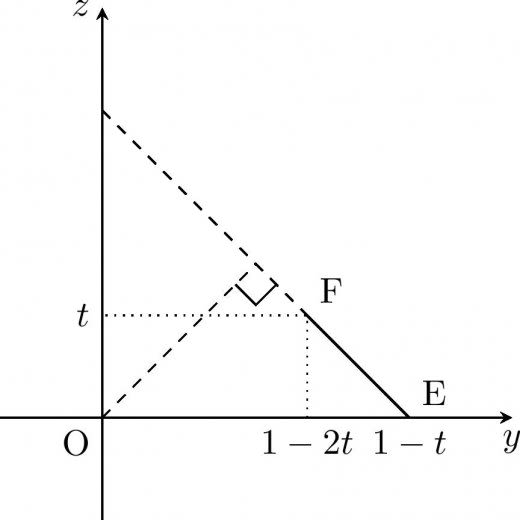
よって面積は
-
のとき
- 軸から最も近い点:
- 軸から最も遠い点:
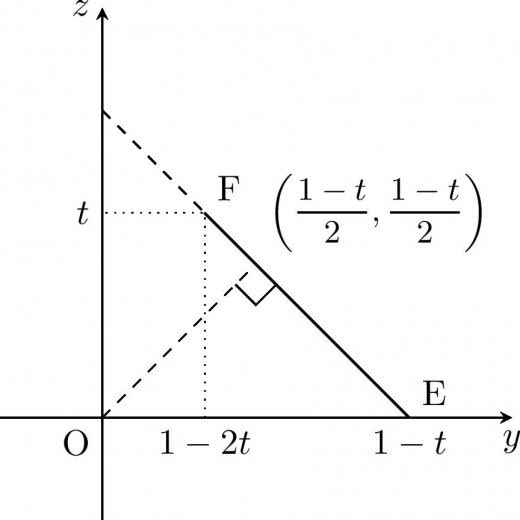
よって面積は
最も近い点が切り替わる のときは三角形 の重心を通過するタイミングです。
さて の場合も調べましょう。
平面 と辺 の交点を とおく。 であるため を得る。
よって は, 上にあり,グラフを描くと次のようになる。
よって
- 軸から最も近い点:
- 軸から最も遠い点:.
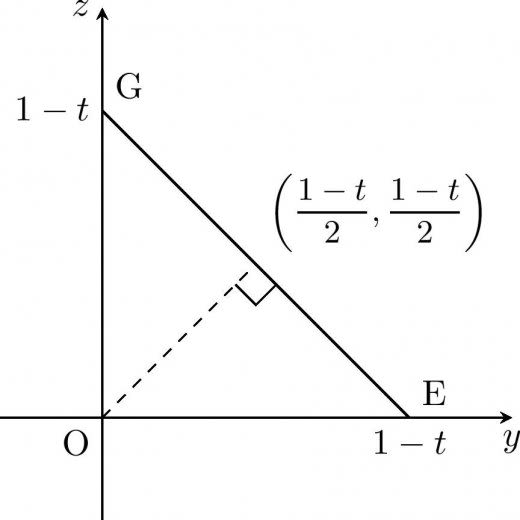
よって,面積は である。
こうして計算できた2つの体積を足し合わせて終了です。
以上より求める体積は である。
-
1項目
-
2項目
よって体積は である。
第六問 [整数]
第六問 [整数]
以上の整数で, とそれ自身以外に正の約数を持たない数を素数という。以下の問いに答えよ。
- とする。 が素数となるような整数 をすべて求めよ。
- を整数の定数とし, とする。 が素数となるような整数 の個数は 個以下であることを示せ。
整数問題を解くメソッドでまずは素直に因数分解をしましょう。
が素数である場合, もしくは となる。
- のとき: は素数である。
- のとき: は素数ではない。
- のとき:
整理すると となるが,これは整数解を持たない。 - のとき:
整理すると となる。これは が解になる。どちらの場合も は素数である。
以上より が求める整数である。
(2) も因数分解から始めましょう。
が素数であるとする。 ( は素数) とおくと, であるため, となる。
よって, が素数 となる が存在する場合,それに応じて 上の点 が対応する。
ここで が素数となる が4つ以上あると仮定する。
は二次関数であるため を満たす は高々2つである。これに注意すると, 上に存在する4点は
- ,,,(ただし )
- ,,,(ただし )
- ,,,
- ,,,(ただし )
- ,,,(ただし )
のいずれかになる。
-
1,2 の場合
増減表を書くと である。 は定数関数ではないため,増減表より から の間に極が存在する。こうして極が少なくとも2つ存在することが分かる。
一方, は二次関数であるため,極は1つしか存在しない。よって矛盾する。 -
3の場合
増減表を書くと である。増減表より と に極が存在する。こうして極が少なくとも2つ存在することが分かる。
一方, は二次関数であるため,極は1つしか存在しない。よって矛盾する。 -
4,5 の場合
1,2の場合の 座標の正負を逆にした場合であるため,同様に矛盾する。 増減表を書くと である。こうして極が少なくとも2つ存在することが分かる。
一方, は二次関数であるため,極は1つしか存在しない。よって矛盾する。
こうして が素数となる は高々3つしかない。
筆者であれば2145と解き,6をちょっと触った後,いったん3を説き伏せると思います。その後6をなんとかするでしょう。
ちなみに6のアイデアは後輩から教えてもらいました。










