【解答・解説】東大理系数学2022
この記事は,今年2022/2/25に実施された「2022年度東京大学入学試験 数学(理系)」の速報・解答解説です。
全体分析
| 項目 | データ |
|---|---|
| 試験日時 | 2022/2/25(金) |
| 試験時間 | 150分 |
| 解答問題数 | 6題 |
| 分量(前年比) | 増加 |
| 難易度(前年比) | 難化 |
| 特徴・傾向 | 状況を正しく把握して立式する能力が中心に試される。 |
大問分析
| 問題番号 | 分野 | 難易度 |
|---|---|---|
| 1 | 微分・積分 | 易 |
| 2 | 整数・数列 | やや難 |
| 3 | 平面図形 | やや易 |
| 4 | 図形と方程式 | やや難 |
| 5 | 空間図形 | 難 |
| 6 | 確率 | 標準 |
※以下の解答・解説,講評等はいずれも東京大学が公表したものではなく,当サイトオリジナルのものです。複数名の現役理系東大生によって作成されています。問題は東京大学第2次試験問題からの引用です。
※当サイトでは「東大英語 2022」の解答・解説も公開しています。
第1問
第1問
次の関数 を考える。
(1) は区間 において最小値を持つことを示せ。
(2) の区間 における最小値を求めよ。
(1)
より,
よって, の増減は以下の通り:
よって, は で最小値を持つ。
(2)
より,
第2問
第2問
数式 を次のように定める。
(1) 正の整数 が の倍数のとき, は の倍数となることを示せ。
(2) を正の整数とする。 が の倍数となるための必要十分条件を を用いて表せ。
(3) と の最大公約数を求めよ。
(1) 数列 は合同式の法を として
のように を繰りかえす。
よって が の倍数のとき, は の倍数となる。
(2)
数列 は単調増加な数列であり, であることに注意すると, が初めて の倍数となるのは のときである。
また, 合同式の法を として
と繰り返す。
すなわち, を で割った余りは、周期を として を繰り返す。
したがって, が の倍数となるための必要十分条件は が の倍数であることである。
(3)
とおく。
であるから, (2)の議論より
となる。
よって, 整数 を用いて と表せる。
すると,
である。
すなわち, と の最大公約数は, と の最大公約数に等しい。
数列 は合同式の法を として
となり, (1)と同様の議論により任意の について は の倍数でない。
一方, は の倍数であるから, (1)より は の倍数である。
したがって, と の最大公約数, すなわち と の最大公約数は である。
が の倍数である が の倍数である
を示す。
まず, すべての について
が成り立つことを数学的帰納法により示す。
のとき
より, は成立する。
ある正の整数 で成り立つと仮定したとき
より でも成り立つ。
以上 より が成り立つ。
を用いると, 正の整数 について, 整数 を用いて
とおくと
となる(ただし のときは と定める)。
よって,
「 が の倍数」 「 が の倍数」
となるが, のとき が の帰納法でわかる。
よって
が の倍数である
が の倍数である
が成立する。
したがって, が の倍数となるための必要十分条件は が の倍数であることである。
第3問
第3問
を原点とする座標平面上で考える。座標平面上の 点 に対し, 点 が点 から十分離れているとは,
が成り立つことと定義する。
不等式
が表す正方形の領域を とし, その つの頂点 を考える。さらに, 次の条件 をともに満たす点 をとる。
点 は領域 の点であり, かつ, 放物線 上にある。
点 は 点 のいずれからも十分離れている。
点 の 座標を とする。
(1) のとりうる値の範囲を求めよ。
(2) 次の条件 をともに満たす点 が存在しうる範囲の面積 を求めよ。
点 は領域 の点である。
点 は 点 のいずれからも十分離れている。
(3) は(1)で求めた範囲で動くとする。(2)の を最小にする の値を求めよ。

上図の赤い部分は 点 から十分離れていない領域を表す。
(1) 上図より
(2) より
である。
のとき
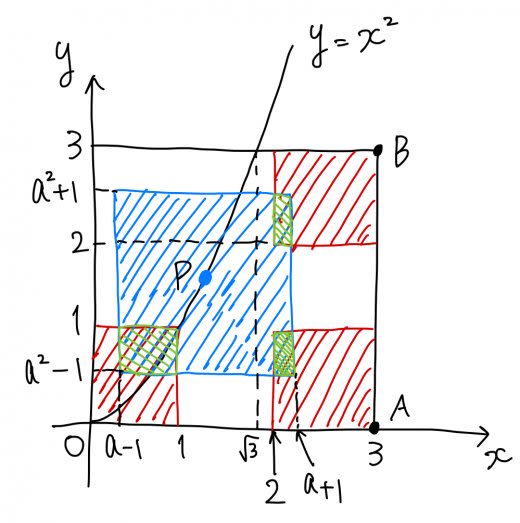
であるから,
のとき

であるから, と同様に考えれば
以上より
(3)
・ のとき
は軸 の下に凸な放物線であり より で である。
・ のとき
よって の増減は以下の通り。
よって を最小にする の値は である。
第4問
第4問
座標平面上の曲線
を考える。
(1) 座標平面上のすべての点 が次の条件 を満たすことを示せ。
点 を通る直線 で, 曲線 と相異なる 点で交わるものが存在する。
(2) 次の条件 を満たす点 のとりうる範囲を座標平面上に図示せよ。
点 を通る直線 で, 曲線 と相異なる 点で交わり, かつ, 直線 と曲線 で囲まれた つの部分の面積が等しくなるものが存在する。
(1) とおく。 を通る直線として,実数 を用いて
を考える。これが と異なる3点で交わる条件は
つまり,
が異なる3つの実数解を持つことである。
以下,このような が必ずあることを示す。
とおく。さて,
ここで , は , のみによる定数である。これより, を十分大きく取れば
となる。よって, の値の増減は次のようになる: よって,中間値の定理より, は異なる3つの実数解を持つ。
(2) として, 上の2点 を通る直線 :
を考える。直線 が直線 と相異なる3点 で交わり, で,かつ直線 と曲線 でかこまれた2つの部分の面積が等しくなることは
と同値である。この式の左辺について より,直線 が条件を満たすことは と同値である。つまり, のもとで,直線 が動く領域を求めれば,それが点 のとりうる範囲となる。
とすると, とできる。よって, は を通る傾き の直線である。 と より だから, は の範囲を動きうる。よって, の動く領域は下図のようになる:

第5問
第5問
座標空間内の点 と 点 を結ぶ線分 を 軸のまわりに 回転させて得られる曲面を とする。 上の点 と 平面上の点 が を満たしながら動くとき, 線分 の中点 が通過しうる範囲を とする。 の体積を求めよ。
の での断面を考える。
点 の 座標が になるのは 点 の 座標が のときである。
よって として良い。
点 のとき, 点 は下図の赤い部分を動く。

よって の での断面は, 上図の赤い円周を のまわりに 回転させてできる図形である。

上図より, 赤い円周は中心が で半径が である。
よって の での断面は以下のようになる。
- のとき

- のとき

よって求める の体積は
ここで, とすると,
であり,また,
であるから,
第6問
第6問
を原点とする座標平面上で考える。 以上の整数 に対して,ベクトル を
と定める。投げたとき表と裏がどちらも の確率で出るコインを 回投げて,座標平面上に点 を以下の規則(i), (ii)に従って定める。
(i) は にある。
(ii) を 以上 以下の整数とする。 が定まったとし, を次のように定める。
-
回目のコイン投げで表が出た場合, により, を定める。ただし, は 回目から 回目までのコイン投げで裏が出た回数とする。
-
回目のコイン投げで裏が出た場合, を と定める。
(1) とする。 が にある確率を求めよ。
(2) とする。 が にあり,かつ,合計 回のコイン投げで表がちょうど 回出る確率を とおく。ただし, である。 を求めよ。また が最大となる の値を求めよ。
まず,問題の条件により,点列 が進む方向は,下図のように分類される。図のように,それぞれ「右向き」,「斜め上向き」,「斜め下向き」と名付ける。
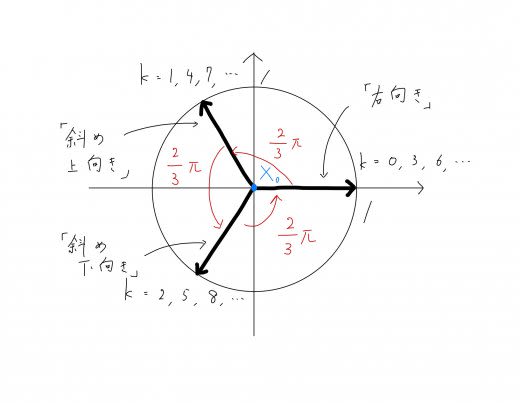
いま,「 回後に点 が原点 にあるためには,右向き、斜め上向き,斜め下向きに動く回数が同じでなければならない」…(*) ことに注意する。
これより「 回後に点 が原点 にあるためには,表が合計で3の倍数回出なければならない」…(**) ということもわかる。
(1)(**)より, 回後に点 が原点 にあることが実現しうるような表と裏の出方は下表のような3通りであることがわかる。
(A)表が0回,裏が8回出るとき
裏が出た時の規則により, 回後に点 は原点 にある。
(B)表が3回,裏が5回出るとき
(*)より,点列は8回の移動の中で,右向き,斜め上向き,斜め下向きにそれぞれ1回ずつ動く。
裏が出たあと,点の進むことができる方向は下図のようになる。

ここで,最上段の数字は裏の出た回数,×印は裏のコインの印,下段の矢印は点列が進む向きを示している(左から1,4番目が「右向き」,2,5番目が「斜め上向き」,3,6番目が「斜め下向き」を表している)。
この裏コインの間に表コインを合計 個配置することを考える.
右向きに進むことができるのは,裏が1回も出ていないときと,裏が3回目に出てから4回目に出るまでであり,その2回のどちらかに1枚表コインを挿入すればよい。よって,右向きに進む進み方は2通り。
斜め上向き,斜め下向きの移動も同様に考えればよい。すなわち,移動できる機会は2回あり,そのいずれかで1回進めばよいから,斜め上向き,斜め下向きに進む進み方は,そのそれぞれで2通り。
したがって, 回後に点 が原点 にあるような裏表の出方は,
通りある。
(C)表が6回,裏が2回出るとき (*)より,点列は8回の移動の中で,右向き,斜め上向き,斜め下向きにそれぞれ2回ずつ動く。
裏が出たあと,点の進むことができる方向は下図のようになる。
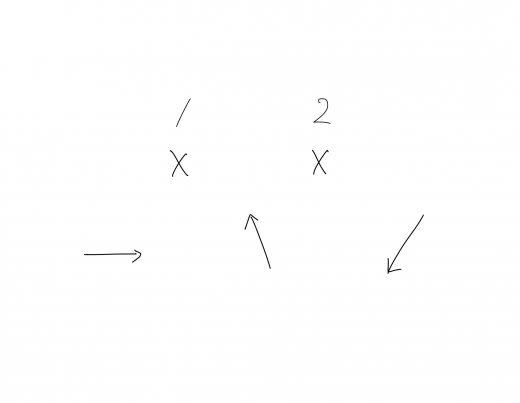
右向きに進むことができるのは,裏が1回も出ていないときであり,そのときに2枚表コインを挿入しなければならない。
斜め上向き,斜め下向きの移動も同様に考えればよい。すなわち,その方向に移動できる機会は1回あり,そのときに2枚表コインを挿入しなければならない。
したがって, 回後に点 が原点 にあるような裏表の出方は1通り。
これらより, 回後に点 が原点 にあるような裏表の出方は合計で
通りある。
また,裏表の出方の総数は
通りあるから,求める確率は
となる。
(2)(**)より, とおいてよい。このとき,表が 回,裏が 回出ることになる。また(*)より右向き、斜め上向き,斜め下向きには各 回動くことになる。
を で割った余りは であることに注意すると,裏が出た後点列が進むことのできる方向は下図のようになる。

上図のように,裏が3回出るごとに点列の進むことができる方向が一巡する。赤線で囲ってある部分の個数は,
組ある。この組1つに対し,右向き、斜め上向き,斜め下向きに動く機会が一度ずつ存在する。
まず,右向きに進む進み方を考える。 組目で右向きに進む回数を とすると,
ただし,各 に対して である。
このような の組の総数は, 通りある。
斜め上向き,斜め下向きについても同様に考えればよく,斜め上向き,斜め下向きに進む進み方は,それぞれ 通りある。
裏表の出方は,合計で 通りあるから、求める確率 は,
となる。
が最大になるような を求めるため,上式より, が最大になるような を求める。 に注意する。
より である。ここで,
だから, が成り立つ。
また,
だから, が成り立つ。以上より, が最大になるような は であることがわかる。したがって, が最大になるような は,
である。
去年に引き続き,今年も難しいセットになりました・・・
受験生の皆さん,気持ちを切り替えて明日も頑張ってください!










