東大数学(図形問題)のポイントと例題
- 難関大の図形問題は「どの道具を使って解答するか」から考える必要があることも。
- 昔の東大入試では簡単な問題も出題されている。
東大の問題とその解説を通じて「図形問題における道具選び」について考えます。
問題
問題
東大1961前期第4問(文理共通問題)です。
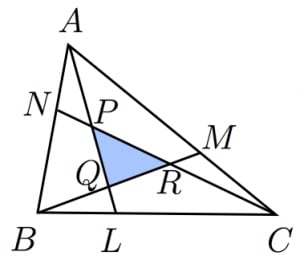
三角形 の各辺 上にそれぞれ を, となるように取る。 と の交点を , と の交点を , と の交点を とするとき三角形 と三角形 の面積比を求めよ。
50年以上も前の問題です!今の東大受験者ならほぼ確実に解けるであろう基本的な問題です。
図形的な考察による解法
図形的な考察による解法
まずはメネラウスの定理(→メネラウスの定理の覚え方と拡張)を用いた解法です。
を求めるのが第一の目標です。そうすれば対称性より他の線分比も分かり,面積比が計算できます。
メネラウスの定理より,
よって,

再びメネラウスの定理より
よって,
この二つの式から が分かる。(→補足)
対称性から なども分かる。
辺の比が分かったので,三角形と面積比の関係を駆使して の面積から の面積を作り出す。
以上3つの式を辺々かけ合わせると を得る。
補足: とおくと,二つの式から , となり,これを解くと を得る。
注:「辺の比が分かれば面積比が分かる」という考え方は重要です。→三角形の面積比にまつわる公式たち
ベクトルによる解法
ベクトルによる解法
次はベクトルを使って機械的な計算で求める方法です。
解答1と同じく を求めに行きます。
, とおき,この二本のベクトルで全てを表していく。

まず, であり,
は 上にあるので( とすると),
と書ける。
これと, が一直線上にあることから
これを解くと となり, を得る。
同じことを について行う( は 上にあり, が一直線上にあることを利用)と を得る。
この二つの情報と対称性より を得る。
以下解答1と同様。
直交座標で計算
直交座標で計算
直交座標を設定しても機械的な計算で解答できますが,この問題の場合計算がわりと複雑になってしまいます。根性がある人はやってみてください。
各道具の特徴
各道具の特徴
(数学オリンピックはもちろんのこと)東大,京大をはじめ,難関大の図形問題はどの道具(図形的な考察orベクトルor座標)を使うのかが不明で自由度が高い問題も出題されます。
したがって,各道具の特徴を知り,問題に合わせて適切に選択する能力も必要になります。
各道具の特徴
図形的な考察:角度の情報に強い,ひらめきが必要な場合が多い,美しい&速い解法が多い
ベクトル:辺の比,平行,中点などの条件に強い,機械的な計算で突破できる,円に弱い,角度の条件に弱い
直交座標:直角に強い,機械的な計算で突破できる,気合いと根性が必要
直交座標は泥臭いので嫌われることが多いですが,私は好きです。











