正多角形の対角線の長さの偶数乗和と積
更新
正 角形 が半径 の円に内接しているとき,以下の1~4が成立する。

3 で とすると1になります。
正方形の例で式の意味を確認したあと,1~4を証明していきます。
正方形で確認
正方形で確認
(正方形)の場合で確認してみましょう。
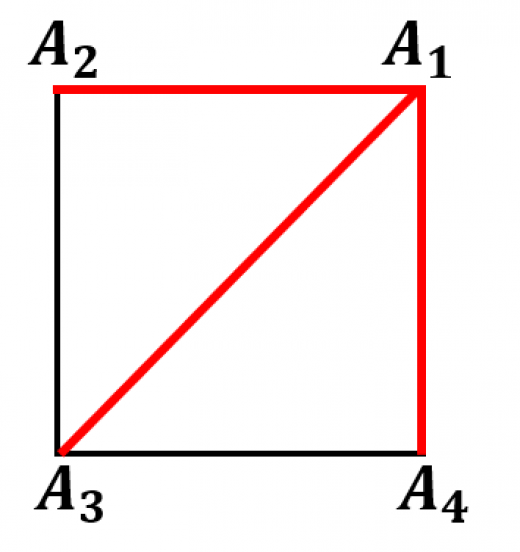
外接円の半径が なので,1辺の長さは です。
です。
- 二乗和は
- 積は
- 4乗和は
- 逆二乗和は
となります!
正三角形や正五角形でも確認してみるとおもしろいです。
- 二乗和の証明
- 二乗和の証明
を証明します。普通の大学入試レベルです。ベクトルを使うのが楽です。
の位置ベクトルを とおく。
ただし,最後の等号では正多角形の対称性より であることを用いた。
- 積の証明
- 積の証明
を証明します。1よりも少し難しいですが入試レベルです。
ここからは複素平面を使います。1の 乗根は単位円周上に等間隔で並ぶことに注意します。(→1のn乗根の性質と複素数平面)
つまり, は複素平面で と表せます。ただし, とおきました。
に注意すると,目標の式の左辺の二乗は
となる。ここで, なので,右辺の1つめの 部分と2つめの 部分は,結局同じものの積になる等しい。よって,目標の式の左辺は と等しい。ここで, は1の 乗根なので, となる。両辺を で割ると, 両辺に を代入すると,赤文字の式が と等しいことがわかる。
- 偶数乗和の証明
- 偶数乗和の証明
ここからかなり難しいです。
を証明します。引き続き複素数平面で考えます。
とおくと,目標の式の左辺は
ただし,最後の等号で を用いた(1のn乗根の性質と複素数平面 の3つめの性質)。
シグマの中身を二項定理で展開すると, となる。
- の項をだけ集めると, となる。ただし,最初の等号は 二項係数の和,二乗和,三乗和 で紹介した有名公式を用いた。
- の各項は, と表せる。ただし, は( には依存するが) には依存しない定数。これを から まで足し上げると, ここで,1つめの等号は,等比数列の和の公式と,( より なので) であることを用いた。2つめの等号は を用いた。
- 逆二乗和の証明
- 逆二乗和の証明
最後に を証明します。引き続き複素数平面で考えます。
3と同様に とおいて左辺を計算すると, となる。分母分子に をかけて部分分数分解すると,上式は
となる。あとは と が計算できればよい。これは たちの基本対称式の値から計算できる。
まず, たちは の解であるので, 両辺 で割って を改めて とすると, 右辺は 次多項式であり,その根が たちなので,解と係数の関係から, の基本対称式の値がわかる。具体的には,右辺を二項定理で展開することで,
より,
- たちの 次の基本対称式(つまり積)は
- たちの 次の基本対称式は
なので,
さらに, たちの 次の基本対称式は
なので,
よって,示すべき式の左辺は
※ を基本対称式で表す部分は少しわかりにくいです。( たちが3つあるとき)で書き下してみると以下になります:
余談
余談
-
逆四乗和も逆二乗和と同様にできそうですが,部分分数分解と対称式の計算が大変そうです。出来た方はぜひ教えてください。
-
3と4の証明は,Twitter で教えてもらったものを自分なりにわかりやすく書き直したものです。証明を教えていただいたみなさま,特に kzy さん,J.Koizumi さん,SSS Education さんの証明を参考にしました,ありがとうございました!
複素数平面のパワーが実感できる話題です。











