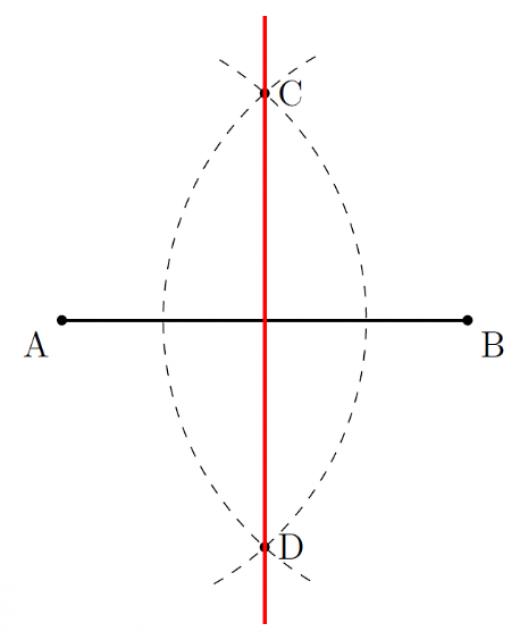
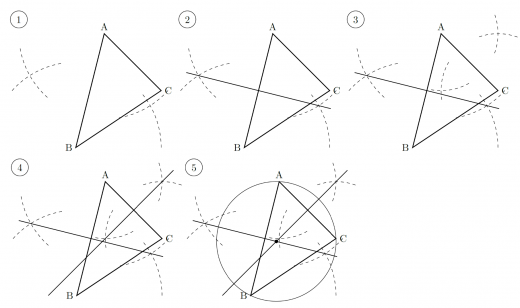
座標平面上に2点が与えられたとき,その垂直二等分線の式を計算しましょう。
定理
座標平面上の2点 A(x1,y1),B(x2,y2) を結んだ線分の垂直二等分線は
(x2−x1)x+(y2−y1)y=2x22−x12+2y22−y12
で与えられる。
覚える必要はないですが,導出できるようになっておきましょう。
まずは素直に直線の式を考える方法から紹介します。
素直に計算をする証明
直線 AB の傾きは x2−x1y2−y1 であるため,垂直二等分線の傾きは −y2−y1x2−x1 である。垂直二等分線は AB の中点 (2x1+x2,2y1+y2) を通る。よって
y=−y2−y1x2−x1(x−2x1+x2)+2y1+y2
となる。整理すると,定理の式を得る。(x1=x2 や y1=y2 のときは傾きの議論は使えないが,定理の式は正しい)
このような計算をするのは骨が折れます。直交することをもう少しうまく使いたいですね。さてここで直交するベクトルの内積が 0 であることを思い出しましょう。
ベクトルを用いた証明
AB の中点を H,垂直二等分線上の任意の点を P(x,y) とおく。AB と HP は直交するため,AB⋅HP=0 である。
P が H と異なるときを考える。
AB=(x2−x1y2−y1)HP=⎝⎛x−2x1+x2y−2y1+y2⎠⎞
であるため内積を計算すると
(x2−x1)(x−2x1+x2)+(y2−y1)(y−2y1+y2)=0
である。式を整理することで求めるべき式が得られる。
またこの式は P が H であるときも含む。
最後に垂直二等分線上の点 P に対して AP=BP であることを用いた方法です。
線分の長さが等しいことを用いた証明
P(x,y) を垂直二等分線上の任意の点とする。このとき AP2=BP2 である。ゆえに
(x−x1)2+(y−y1)2=(x−x2)2+(y−y2)2
である。
x2−2x1x+x12+y2−2y1y+y12=x2−2x2x+x22+y2−2y2y+y222{(x2−x1)x+(y2−y1)y}=x22−x12+y22−y12(x2−x1)x+(y2−y1)y=2x22−x12+2y22−y12
である。
 手順1:コンパスで点 ,点 を中心とした同じ半径の円弧を描く
手順1:コンパスで点 ,点 を中心とした同じ半径の円弧を描く