京大理系数学2020入試過去問解答解説
※以下の解答と解説は京都大学が公表したものではなく,当サイトオリジナルのものです。問題は京都大学第2次試験問題からの引用です。
この記事では,京都大学の2020年度入学試験の理系数学について解説します。
第一問[複素数平面]
第一問[複素数平面]
は実数で, とする。 に関する方程式 は つの相異なる解を持ち,それらは複素数平面上で一辺の長さが の正三角形の頂点となっているとする。このとき, と の つの解を求めよ。
複素数平面の問題です。与えられた方程式は実数係数の多項式で形成されたものになっているので,共役複素数の性質が使えて,解を と置くことができます。 →共役複素数の覚えておくべき性質
また,辺の長さが決まっていることを利用すれば, は で簡単に表すことができます。これと解と係数の関係をうまく組み合わせていけば,答えを導くことができます。
は実数係数の方程式なので,解を とおける。 の虚部は正であるとする。このとき, は実軸に対して対称であるから, が正三角形をなすには が実数であることが必要である。
については以下の図の (i),(ii) のような位置にあることが考えられる。
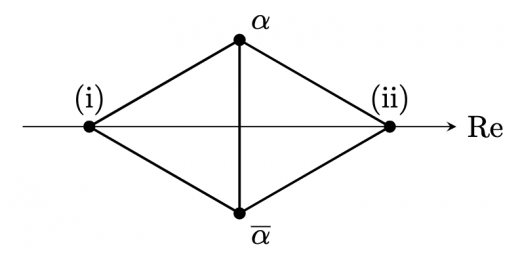
また,解と係数の関係より, が成立する。
(i) 図より, にこれを代入して整理すると, これより, これらを に代入して整理すると, さらに, より,
(ii) 図より, にこれを代入して整理すると, これは明らかに の解にはならないので不適。
(i),(ii)より, また, つの解は すなわち
第二問[整数・極限]
第二問[整数・極限]
を整数とする。 は に関する方程式 の つの解で, であるとする。
(1) すべての正の整数 に対し, は整数であり,さらに偶数であることを証明せよ。
(2) 極限 を求めよ。
(1)はあまり難しくありません。数学的帰納法を使うだろうと予測できると思います。ただ,「一つ前だけでなく二つ前も仮定するパターン」の数学的帰納法を利用しなければなりません。→数学的帰納法をわかりやすく【例題3問、応用5パターン】
数学的帰納法により示す。与えられた方程式において解と係数の関係を使えば,
(i) のとき より,これは偶数である。
(ii) のとき より,これは偶数である。
(iii) のとき は偶数であると仮定する。このとき, は全て偶数であるから, も偶数である。
(i),(ii),(iii)より,数学的帰納法から題意は示された。
(2)はやや難しいかもしれません。 より, は発散してしまうので, は振動してしまいます。 を含む極限の公式 を利用するには, の中身が のとき に近づかなければなりません。
ここで,解と係数の関係を使うと, であることがわかります。もし の中身を で置き換えることができたら,この公式が使えるかもしれません。この置き換えに際し,(1)での結果が利用できます。
の判別式を とすると, であるから, は実数である。ここで より, であり, であるから,
ここで, は偶数より, より, であるから,
第三問[空間図形・ベクトル]
第三問[空間図形・ベクトル]
の正の実数とする。座標空間において,原点 を中心とする半径 の球面上の 点 が次の関係式を満たしている。 このとき, の値を求めよ。ただし,座標空間の点 に対して, は, と の内積を表す。
空間図形の問題です。文系の第四問と共通の問題です。詳しい解説は以下の記事からご覧ください。→京大文系数学2020入試過去問解答解説
座標空間をうまく置けるかが鍵になってきます。対称性を意識して計算を楽にできるような座標をおくことを考えてみましょう。
第四問[整数]
第四問[整数]
正の整数 に対して, の形に書いたとき, と定める。例えば, である。
は整数で,次の条件を満たすとする。
(i) 。
(ii) 。
(iii) は で割り切れない。
このような について とするとき, の最大値を求めよ。また, の最大値を与えるような をすべて求めよ。
などを使って複雑に定義されていますが,結局やりたいことは で割り切れる回数の最大値は何でしょう?という問題です。 で割ったあまりを求めたいので, で割ったあまりで場合わけをして考えるのが良さそうです。
以下合同式において を法とする。
(i) のとき
(i-i) のとき より, は で割り切れないので,
(i-ii) のとき より,
(i-iii) のとき より, は で割り切れないので,
(ii) のとき (i-i),(i-ii),(i-iii)と同様に考えれば,
(ii-i) のとき
(ii-ii) のとき
(ii-iii) のとき
(i),(ii)より, のとき は最大値を取りうる。 として,場合わけして考える。
以下の合同式では を法とする。
を で割ったあまりについて表をつくると以下のようになる。
よって は では割り切れないので,
を で割ったあまりについて表をつくると以下のようになる。
これより, のとき は最大値を取りうる。 の値について場合わけして考える。
のとき
は の倍数ではないので
のとき
よって
のとき
は の倍数ではないので
のとき
は の倍数ではないので
これより, のとき は最大値を取りうる。
合同式において,以下再び を法とすれば, のとき,合同式において再び を法として よって, のとき は最大値 をとる。
記述は長くなってしまいましたが,やっていることは単純です。
第五問[場合の数]
第五問[場合の数]
縦 個,横 個のマス目のそれぞれに の数字を入れていく。このマス目の横の並びを行といい,縦の並びを列という。どの行にも,どの列にも同じ数字が 回しか現れない入れ方は何通りあるか求めよ。下図はこのような入れ方の 例である。

場合の数の問題です。文系の第五問と共通の問題です。詳しい解説は以下の記事からご覧ください。→京大文系数学2020入試過去問解答解説
対称性を利用すれば,数え上げて解けてしまう問題です。理系の京大受験生ならばサクッと解けてほしい問題だと思います。
第六問[体積・積分]
第六問[体積・積分]
を座標とする空間において, 平面内の曲線 を 軸のまわりに 回転させるとき,この曲線が通過した部分よりなる図形を とする。この をさらに 軸のまわりに 回転させるとき, が通過した部分よりなる立体を とする。このとき, の体積を求めよ。
求積の問題です。
より,与えられた曲線は 平面上の原点から まで単調増加で立ち上がる曲線になります。よって, なる実数 を用いて で を切った断面は円となり, を動かせば は数式で表現できます。
数式で が表されれば,あとは の による断面を考えて面積を求め,それを で定積分すれば答えが出るはずです。
のとき
は単調増加する関数であり, より,与えられた曲線の概形を 平面に図示すると以下の通り。
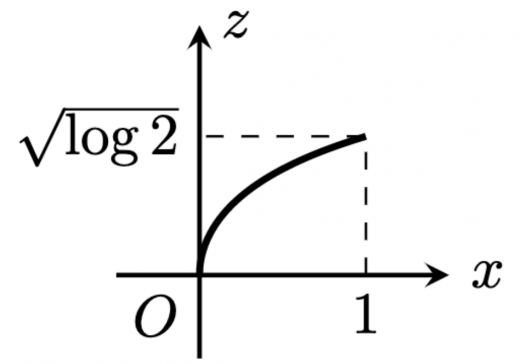
なる実数 を用いて, における の断面を考える。 より, における の断面の方程式は, よって, は で表される。 のもとで, は と変形される。 なる実数 を用いて, における の断面を考える。 の断面の方程式は で表される。 は に関して偶関数であり, においては単調増加関数である。概形は以下の通り。
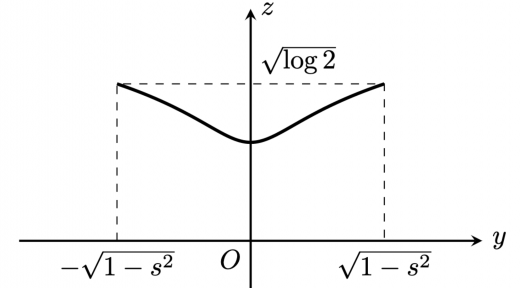
これを 軸を中心に 回転させると,大きい円から,同心円である小さい円をくり抜いた形をした, の断面となる。内径は ,外径は である。これより, における の断面の面積は よって, の体積 は,
方針で迷うことはないと思いますが,計算が大変ですね。
京都大学二次試験理系数学2020入試問題解答解説まとめ
京都大学二次試験理系数学2020入試問題解答解説まとめ
シンプルな問題設定なのに,発想力が求められる,という問題が京大ではよく出題されます。ただ,その中でも取りやすい問題はセットのなかに必ず紛れています。今回で言えば,第一問,第二問(1),第三問,第五問のような問題です。
また,第六問も計算は大変ですが,方針を立てること自体は,よく勉強されている方なら難しくなかったと思います。体積の問題は大学入試では頻出であり,特に東大も好んで出します(2018の東大理系6番は私のお気に入りの問題です→東大理系数学2018入試過去問解答解説)。東大の問題は京大に比べると計算量が多めですが,勉強に使うのにとてもおすすめです。
まずは教科書レベルの問題を真剣に取り組み,数学の概念を深く理解しましょう。その後は,京大の過去問をはじめとする難関校の過去問に触れてみると良いでしょう。
引き続き,数学の学習に頑張って取り組んでください。
最近の大学の問題は難易度が高めのものが増えている気がします。









