京大文系数学2020入試過去問解答解説

$$f(x) = |x|x -3x + 1$$ とおくと， $$f(x) = \begin{cases} x^2 -3x + 1 & (x \geq 0)\\ -x^2 -3x + 1 & (x < 0)\\ \end{cases}$$ これを図示すると，下図のようになる。

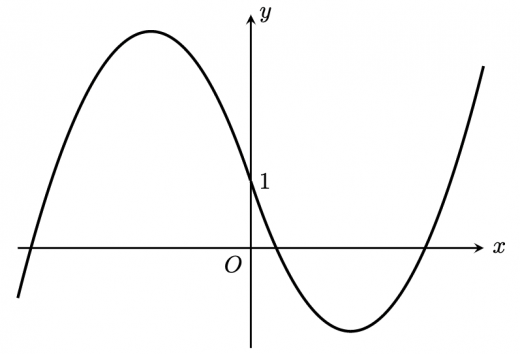
$a$ は負，つまり $l$ の $y$ 切片は負であるから，グラフより $l$ は $C$ の $x \geq 0$ の部分と接する。 $$y = x^2 -3x + 1$$ と $$y = x + a$$ について，これらを連立して， $$\begin{aligned} x^2 - 3x + 1 &= x + a\\ \therefore x^2 -4x + 1 -a &= 0 \end{aligned}$$ この方程式の判別式を $D$ とすれば， $$\dfrac{D}{4} = 2^2 - (1-a) = 3 + a$$ $D = 0$ のとき，$C$ と $l$ は接する。 $$\begin{aligned} 3 + a &= 0\\ \therefore a &= -3 \end{aligned}$$ このとき，共有点は $$\begin{aligned} x^2 -3x + 1 &= x - 3\\ (x-2)^2 &= 0\\ x = 2 \end{aligned}$$ また， $$\begin{aligned} -x^2 -3x + 1 &= x-3\\ x^2 + 4x -4 &= 0 \end{aligned}$$ $x < 0$ より， $$x = -2 -2\sqrt{2}$$ これより，$C$ と $l$ を図示すると，下図のようになる。

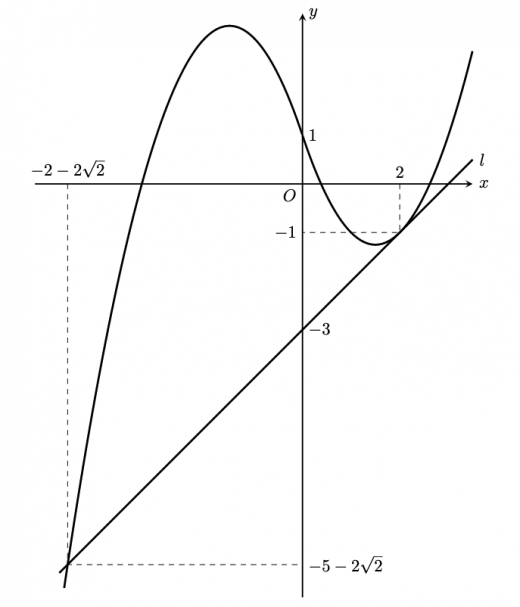
よって，求める面積 $S$ は， $$\begin{aligned} S &= \int_{-2-2\sqrt{2}}^0 \left\{(-x^2 -3x + 1) - (x-3)\right\}dx\\ & \quad \quad + \int_0^2 \left\{(x^2 -3x + 1)-(x-3)\right\}dx\\ &= \int_{-2-2\sqrt{2}}^0 \left\{-(x+2)^2 + 8\right\}dx\\ & \quad \quad + \int_0^2 (x-2)^2dx\\ &=\left[-\dfrac{1}{3}(x+2)^3 + 8x\right]_{-2-2\sqrt{2}}^0 + \left[\dfrac{1}{3}(x-2)^3\right]_0^2\\ &= -\dfrac{8}{3} - \left(-\dfrac{1}{3}(-2\sqrt{2})^3 + 8(-2-2\sqrt{2})\right) + \dfrac{8}{3}\\ &= 16 + \dfrac{32\sqrt{2}}{3} \end{aligned}$$

問題の条件を満たす2次関数を $$f(x) = ax^2 + bx + c$$ とおく。ただし， $$a \neq 0 \tag{1}$$ $x = t$ において，$y = x^2$ と $y = f(x)$ が直交することは，以下のように表現される： $$\begin{aligned} f(t) &= t^2\\ f'(t)\cdot 2t &= -1 \end{aligned}$$ これを整理すれば， $(2)$ について，$y = x^2$ と $y = f(x)$ は $2$ 点で交わるはずなので， $$a \neq 1 \tag{4}$$ が必要である。このもとで，$(2)$ かつ $(3)$ は と同値である。$(5),(6)$ は $2$ 解 $\alpha, \beta ~~ (\alpha < \beta)$ をもつので， が成立している必要がある。解が共通であることを考えれば，$(5),(6)$ はどちらも $$(t-\alpha)(t-\beta) = 0$$ と変形できる。よって，恒等的に $$t^2 + \dfrac{b}{a-1}t + \dfrac{c}{a-1} = t^2 + \dfrac{b}{2a}t + \dfrac{1}{4a}$$ が成立する。したがって， この問題は，$(1),(4),(7),(8),(9),(10)$ を全て満たす $a,b,c$ の条件をもとめることに帰着される。

$a \neq 0, a \neq 1, (10)$ より， $$c \neq 0$$ よって，$(9) \div (10)$ ができて， $$\dfrac{b}{c} = 2b\\ \therefore b(1-2c) = 0$$

(i) $b = 0$ のとき

$(10)$ より， $$c = \dfrac{a-1}{4a}$$ $(7)$ より， $$-\dfrac{4c}{a-1} > 0\\ -\dfrac{4}{a-1}\cdot\dfrac{a-1}{4a} > 0\\ \therefore a < 0$$ これらが満たされるとき，$(1),(4),(8),(9)$ は自動的に満たされる。

(ii) $c = \dfrac{1}{2}$ のとき

$(10)$ より， $$a = -1$$ これらが満たされるとき，$(1),(4),(7),(8),(9)$ は自動的に満たされる。

よって，(i),(ii) より，任意の負の実数 $a$ と，任意の実数 $b$ を用いて， $$\begin{cases} y = ax^2 + \dfrac{a-1}{4a}\\ y = -x^2 + bx + \dfrac{1}{2} \end{cases}$$ とかける。

$m$ が奇数，$n$ が偶数のとき，$mn^2$ は偶数，$am^2$ は奇数，$n^2$ は偶数となるから，$mn^2 + am^2 + n^2 + 8$ は奇数となって，$16$ の倍数にはなり得ない。

$m$ が偶数，$n$ が奇数のとき，$mn^2$ は偶数，$am^2$ は偶数，$n^2$ は奇数となるから，$mn^2 + am^2 + n^2 + 8$ は奇数となって，$16$ の倍数にはなり得ない。

$m$ が奇数，$n$ が奇数のとき，$mn^2$ は奇数，$am^2$ は奇数，$n^2$ は奇数となるから，$mn^2 + am^2 + n^2 + 8$ は奇数となって，$16$ の倍数にはなり得ない。

これより，$m,n$ は偶数となることが必要なので，整数 $k,l$ を用いて， $$\begin{cases} m = 2k\\ n = 2l \end{cases}$$ と置く。このとき $$\begin{aligned} f(m,n) &= 2k\cdot 4l^2 + a\cdot 4k^2 + 4l^2 + 8\\ &= 4(2kl^2 + ak^2 + l^2 + 2) \end{aligned}$$

よって，$2kl^2 + ak^2 + l^2 + 2$ が $4$ の倍数となれば良い。

$k$ が偶数のとき，$ak^2$ は偶数，$2kl^2 + 2$ は偶数より，$2kl^2 + ak^2 + l^2 + 2$ が $4$ の倍数となるには，$l^2$ は偶数になる必要がある。整数 $p,q$ を用いて $$\begin{cases} k = 2p\\ l = 2q \end{cases}$$ とおけて， $$\begin{aligned} f(m,n) &= 4(2\cdot 2\cdot 4q^2 + a\cdot 4p^2 + 4q^2 + 2)\\ &= 4\left\{4(4pq^2 + ap^2 + q^2) + 2\right\} \end{aligned}$$ $4(4pq^2 + ap^2 + q^2) + 2$ は $4$ の倍数になり得ないので不適。

$k$ が奇数のとき，$ak^2$ は奇数，$2kl^2 + 2$ は偶数より，$2kl^2 + ak^2 + l^2 + 2$ が $4$ の倍数となるには，$l^2$ は奇数になる必要がある。整数 $p,q$ を用いて $$\begin{cases} k = 2p + 1\\ l = 2q + 1 \end{cases}$$ とおけて， $$\begin{aligned} f(m,n) &= 4(2\cdot (2p+1)\cdot(2q + 1)^2 + a\cdot (2p+1)^2 + (2q + 1)^2 + 2)\\ &= 4\left\{(4 \text{の倍数}) + 1 + a\right\} \end{aligned}$$ よって，$a + 1$ が $4$ の倍数となればよく，整数 $s$ を用いて， $$a = 4s - 1$$ と書けることが条件となる。

座標空間を $$\begin{cases} A(1,0,0)\\ B(s,t,0) \end{cases}$$ となるように取ることができる。 $$\overrightarrow{OA}\cdot \overrightarrow{OB} = \dfrac{1}{2}$$ より， $$s = \dfrac{1}{2}$$ また，$B$ は半径 $1$ の球面上にあることから， $$\begin{aligned} s^2 + t^2 &= 1\\ \therefore t &= \pm\dfrac{\sqrt{3}}{2} \end{aligned}$$ 対称性から，正負のどちらを採用しても $k$ の値は同じなので，ここでは $$t = \dfrac{\sqrt{3}}{2}$$ を採用して議論を進める。つまり，$B\left(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2}, 0\right)$ である。$C(a,b,c)$ とおく。$\overrightarrow{OA} \cdot \overrightarrow{OC} = -\dfrac{\sqrt{6}}{4}$ より， $$a = -\dfrac{\sqrt{6}}{4}$$ $\overrightarrow{OB} \cdot \overrightarrow{OC} = -\dfrac{\sqrt{6}}{4}$ より， $$\dfrac{1}{2}a + \dfrac{\sqrt{3}}{2}b = -\dfrac{\sqrt{6}}{4}$$ これらにより， $$a = -\dfrac{\sqrt{6}}{4}, ~ b = -\dfrac{\sqrt{2}}{4}$$ また，$C$ は半径 $1$ の球面上にあることから， $$\begin{aligned} a^2 + b^2 + c^2 &= 1\\ \therefore c &= \pm \dfrac{1}{\sqrt{2}} = \pm \dfrac{\sqrt{2}}{2} \end{aligned}$$

(i) $c = \dfrac{\sqrt{2}}{2}$ のとき

$C\left(-\dfrac{\sqrt{6}}{4},-\dfrac{\sqrt{2}}{4}, \dfrac{\sqrt{2}}{2}\right)$ である。$D(x,y,z)$ とおいたとき， $$\begin{cases} \overrightarrow{OC}\cdot\overrightarrow{OD} = \dfrac{1}{2}\\ \overrightarrow{OA}\cdot\overrightarrow{OD} = \overrightarrow{OB}\cdot\overrightarrow{OD} = k\\ C \text{は半径} 1 の球面上にあること \end{cases}$$ より， $(2),(3)$ より， $$x = k, ~~ y = \dfrac{1}{\sqrt{3}}k$$ これらを $(1)$ に代入し， $$\begin{aligned} \dfrac{\sqrt{2}}{2}z &= \dfrac{1}{2} + \dfrac{\sqrt{6}}{4}k + \dfrac{\sqrt{2}}{4}\cdot \dfrac{1}{\sqrt{3}}k\\ \therefore z &= \dfrac{\sqrt{2}}{2} + \dfrac{2\sqrt{2}}{3}k \end{aligned}$$ よって，$(4)$ より， $$\begin{aligned} k^2 + \dfrac{1}{3}k^2 + \left(\dfrac{\sqrt{2}}{2} + \dfrac{2\sqrt{2}}{3}k\right)^2 &= 1\\ 16k^2 + 4\sqrt{6}k - 3 &= 0\\ k = \dfrac{-2\sqrt{6} \pm 6\sqrt{2}}{16} \end{aligned}$$ $k > 0$ より， $$k = \dfrac{-2\sqrt{6} + 6\sqrt{2}}{16}$$

(ii) $c = -\dfrac{\sqrt{2}}{2}$ のとき

(i)の $z$ に対し，$z \to -z$ とすればよく， $$z = -\dfrac{\sqrt{2}}{2} -\dfrac{2\sqrt{2}}{3}k$$ これは $(4)$ に代入すれば，$2$ 乗されて符号は相殺されるので， $$k = \dfrac{-2\sqrt{6} + 6\sqrt{2}}{16}$$

よって，(i),(ii) より， $$k = \dfrac{-2\sqrt{6} + 6\sqrt{2}}{16}=\dfrac{-\sqrt{6}+3\sqrt{2}}{8}$$

対称性により，1行目を左から順に $1,2,3,4$ としてその場合の数 $N$ を求め，$N$ を $4!$ 倍したものが求める場合の数である。

さらに対称性より，1列目を上から順に $1,2,3,4$ としてその場合の数 $M$ を求め，$M$ を $3!$ 倍したものが $N$ となる。

上から $n$ 行目，左から $m$ 列目のことを $(n,m)$ とかくことにする。

(i) $(2,2)$ に $1$ があるとき

2行目は $2,1,4,3$ に決まる。$(3,2)$ には $4$ が入ることが決まる。これより3行目は $3,4,1,2$ か $3,4,2,1$ の $2$ 通りがある。4行目は3行目によって一意に定まる。

(ii) $(2,2)$ に $3$ があるとき

2行目は $2,3,4,1$ に決まる。3行目も $3,4,1,2$ で一意に決まる。4行目も3行目によって一意に定まる。

(iii) $(2,2)$ に $4$ があるとき

2行目は $2,4,1,3$ に決まる。3行目も $3,1,4,2$ で一意に決まる。4行目も3行目によって一意に定まる。

(i),(ii),(iii) により， $$M = 4$$ よって求めたい場合の和は $$4 \times 3! \times 4! = 576$$ 通りである。