ビュフォンの針の問題と確率の導出

さきほどの図より，
針が線と交わる（共有点を持つ）$\iff y \leq \dfrac{l}{2}\sin\theta$

よって，$y$ と $\theta$ をランダムに決めたときに $y\leq \dfrac{l}{2}\sin\theta$ となる確率を求めればよい。

「ランダムに $y$ と $\theta$ を選ぶ」ことは「図の長方形内にランダムに一つ点を取る」ことに対応する。よって，求める確率は図において （青い部分の面積）÷（長方形の面積）である。

長方形の面積は $\dfrac{\pi d}{4}$ であり，青い部分の面積は $\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{l}{2}\sin\theta d\theta=\dfrac{l}{2}$ であるので，求める確率は $\dfrac{2l}{\pi d}$ となる。

$l\leq d$ の場合と考え方は同じ。求める確率は図において （青い部分の面積）÷（長方形の面積）である。

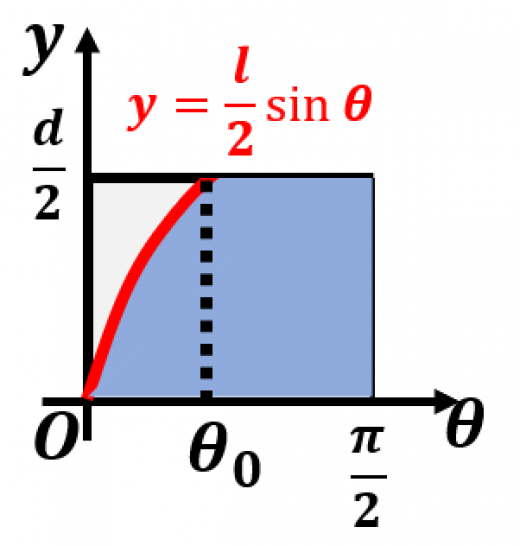
ただし，$\theta_0$ は $\dfrac{l}{2}\sin\theta_0=\dfrac{d}{2}$ を満たす。

長方形の面積は $\dfrac{\pi d}{4}$ であり，青い部分の面積は $\displaystyle\int_0^{\theta_0}\dfrac{l}{2}\sin\theta d\theta+(\dfrac{\pi}{2}-\theta_0)\cdot\dfrac{d}{2}\\ =\dfrac{l}{2}(-\cos\theta_0+1)+\dfrac{\pi d}{4}-\dfrac{d\theta_0}{2}$

つまり，求める確率は

$\dfrac{2l}{\pi d}(1-\cos\theta_0)+1-\dfrac{2\theta_0}{\pi}\\ =\dfrac{2l}{\pi d}-\dfrac{2l}{\pi d}\sqrt{1-\sin^2\theta_0}+1-\dfrac{2\theta_0}{\pi}\\ =\dfrac{2l}{\pi d}\left(1-\sqrt{1-\dfrac{d^2}{l^2}}\right)+1-\dfrac{2}{\pi}\mathrm{Arcsin}\left(\dfrac{d}{l}\right)$