円と正多角形の間の等周問題~東北大学AO2022
を3以上の整数とする。正 角形 の周の長さと円 の周の長さが等しいとき, の面積 と の面積 の大小を比べよ。
東北大学AO試験の問題です。等周問題に関する問題です。
解答の前に
解答の前に
この問題のように,「周の長さが同じ図形の中で面積が大きいものはどんなものか」を考える問題を等周問題といいます。
詳しくは 等周問題に関連する高校数学の問題 をご覧ください。
実は,次の定理が成り立ちます。
周の長さが一定である図形の中で面積が最大のものは円である。
一般の場合の証明は大変ですが,正多角形と比較する場合は簡単です。
解答
解答
周長を として計算してよい(周長を 倍すると,面積 はいずれも 倍になるので)。
- の計算
の中心を とする。頂点には反時計回りに と番号を付ける。
このとき である。
は底辺の長さが ,頂角が の二等辺三角形である。
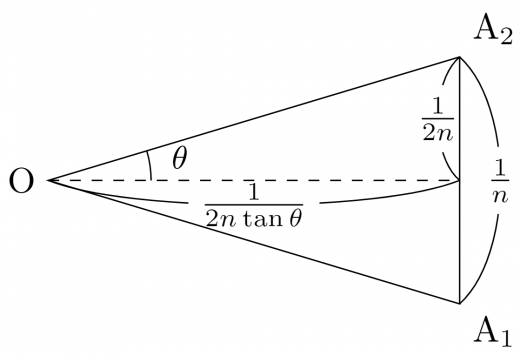
よってその面積は である。
- の計算
周長が であるため半径は である。よって となる。
- 比較
と の比較をすればよい。
実数 について,次が成り立つ。 → 注
この不等式を用いると, である。
よって を得る。
注:これは所謂 マクローリン型の不等式 です。証明は微分するだけなので簡単です。
とする。 である。( に注意)
よって は単調に増加するため ,つまり である。(証明終了)
おまけ: 角形同士の比較
おまけ: 角形同士の比較
円のほうが面積が大きいことは分かりました。
それでは正多角形同士で面積の大小はどのようになっているのでしょうか。以下,周長 の正 角形の面積を とおきましょう。
でした。この分母の増減を調べます。
ですので, をかたまりと見て, の増減を調べれば良さそうです。
とする。 とおく。
一般に であるため である。
よって は単調に増加する。
これより は単調に減少し, は単調に増加することが分かる。
こうして が大きくなればなるほど面積は大きくなると分かりました。
正 角形の を大きくしていくと,どんどん円に近付くので納得できる結果ですね。
今回は計算に使いませんでしたが, であることにも注意しておきたいですね。
東北大学のAO入試はシンプルでおもしろい問題が多いです。











