多様体入門4～接ベクトル

更新 2025/09/24

接ベクトル

接ベクトルとは，多様体の局所的な情報を持つベクトル空間である。

導入：速度ベクトル

接線と速度ベクトルグラフの局所的な変動は接線によって表されます。
しかし一般的な多様体で接線をどう考えればよいでしょうか？ 速度に着目してみましょう。
 \:
例えば，点 P\mathrm{P}P が曲線 CCC 上を動いているとしましょう。
このとき，CCC 上のある点 A\mathrm{A}A 上に差し掛かったとき，点 P\mathrm{P}P の移動方向のベクトルは接線に沿っています。
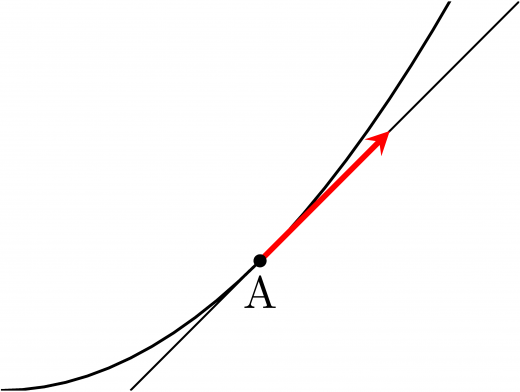
接線上の各点は，グラフ上を動く点の速度に対応していると思うことができます。
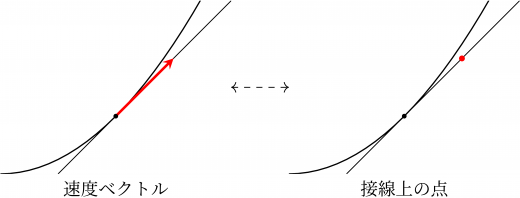
ユークリッド空間における速度ベクトル位置ベクトル
x(t) (−ε≦t≦ε)x(t) \: (-\varepsilon \leqq t \leqq \varepsilon)x(t)(−ε≦t≦ε) を考えます。
位置ベクトルの t=0t=0t=0 での速度ベクトルは
lim⁡t→0x(t)−x(0)t
\lim_{t \to 0} \dfrac{x(t) - x(0)}{t}
t→0lim​tx(t)−x(0)​
と定義されます。
例
x(t)=(tt2) (t∈R)x(t) = \begin{pmatrix} t \\ t^2 \end{pmatrix} \: (t \in \mathbb{R})x(t)=(tt2​)(t∈R) とするとき，t=0t = 0t=0 のときの速度ベクトルは (10)\begin{pmatrix} 1\\0 \end{pmatrix}(10​) である。
今は Rn\mathbb{R}^nRn 上で動く点の速度ベクトルでしたので，より一般に CrC^rCr 級多様体 MMM 上を動く点の速度ベクトルを考察します。

多様体上の速度ベクトルの考え方

前節を思い出せばユークリッド空間内であれば速度ベクトルが計算できることが分かります。多様体は局所的にユークリッド空間とみなせるため，都合よく速度ベクトルを計算することができそうです。
多様体上の「位置ベクトル」MMM を mmm 次元 CrC^rCr 級多様体とします。MMM の点 ppp を任意に取ります。
位置ベクトルの代わりに CrC^{r}Cr 級写像 ccc を考えます。 ccc は
c:(−ε,ε)→Mc(0)=p\begin{aligned}
c : (-\varepsilon , \varepsilon) &\to M\\
c(0) &= p
\end{aligned}c:(−ε,ε)c(0)​→M=p​
を満たすものとします。（以下 MMM 上の曲線と呼ぶこともあります。）
ccc は「位置」と考えることができます。ccc の「導関数」を見ることで速度ベクトルを計算しましょう。
ppp を含む座標近傍 (U,ϕ,V)(U,\phi , V)(U,ϕ,V) を取ります。
このとき，
ϕ∘c:(−ε,ε)→V⊂Rm
\phi \circ c : (-\varepsilon , \varepsilon) \to V \subset  \mathbb{R}^m
ϕ∘c:(−ε,ε)→V⊂Rm
となります。
ϕ∘c\phi \circ cϕ∘c はユークリッド空間における位置ベクトルになっています。そのため，前節のようにして速度ベクトルを考えることができます。つまり，
ddt(ϕ∘c)∣t=0=lim⁡t→0ϕ∘c(t)−ϕ∘c(0)t
\left. \dfrac{d}{dt} (\phi \circ c) \right|_{t=0} = \lim_{t \to 0} \dfrac{\phi \circ c (t) - \phi \circ c(0)}{t}
dtd​(ϕ∘c)∣∣​t=0​=t→0lim​tϕ∘c(t)−ϕ∘c(0)​
により mmm 次元の速度ベクトルを計算することができました。
座標近傍に寄らない方法以上での議論では，ccc の速度ベクトルを考える上で ppp 周りの座標近傍を1つ固定して計算をしました。次は，座標近傍に寄らずに速度ベクトルを計算する方法を探してみましょう。
∗∗∗
\ast\ast\ast
∗∗∗
突然ですが，CrC^rCr 級関数 f:M→Rf : M \to \mathbb{R}f:M→R を任意に考えます。（本当に任意でよいです）
曲線と合成することで CrC^rCr 級関数
f∘c:(−ε,ε)→R
f \circ c : (-\varepsilon , \varepsilon) \to \mathbb{R}
f∘c:(−ε,ε)→R
が得られます。これの t=0t = 0t=0 における導関数
ddt(f∘c)∣t=0
\left. \dfrac{d}{dt} (f \circ c) \right|_{t = 0}
dtd​(f∘c)∣∣​t=0​
を考えてみましょう。
計算過程で座標近傍を取らなかったので，この量は座標近傍に寄らず定まります。
ccc に対して，関数 fff から R\mathbb{R}R を対応付ける写像
f↦ddt(f∘c)∣t=0
f \mapsto \left. \dfrac{d}{dt} (f \circ c) \right|_{t = 0}
f↦dtd​(f∘c)∣∣​t=0​
を ccc の t=0t=0t=0 における方向微分といいます。
簡単な定義
点 ppp における MMM の接ベクトル空間を，方向微分全体の集合と定める。
つまるところ，接ベクトル空間 MMM の ppp における速度ベクトルの集合を，写像によって定めている。
点 p 近傍の曲線 c⇝方向微分
\text{点} \ p \ \text{近傍の曲線} \ c \rightsquigarrow \text{方向微分} 
点 p 近傍の曲線 c⇝方向微分

接ベクトル空間の定義1

これまでの議論を元に，より厳密な定義を書き下します。
接ベクトルの定義1
MMM を多様体とし，点 p∈Mp \in Mp∈M を固定する。
2つの CrC^rCr 級写像 c,c′:(−ε,ε)→Mc,c' : (-\varepsilon , \varepsilon) \to Mc,c′:(−ε,ε)→M の間に同値関係 c∼c′c \sim c'c∼c′ を
任意の p∈Mp \in Mp∈M の近傍で定義された CrC^rCr 級写像 f:M→Rf : M \to \mathbb{R}f:M→R に対して 
ddt(f∘c)∣t=0=ddt(f∘c′)∣t=0
\left. \dfrac{d}{dt} (f \circ c) \right|_{t=0} = 
\left. \dfrac{d}{dt} (f \circ c') \right|_{t=0}
dtd​(f∘c)∣∣​t=0​=dtd​(f∘c′)∣∣​t=0​
が成り立つ
このとき，MMM の ppp における接ベクトル空間 TpMT_p MTp​Mを

{c:(−ε,ε)→M∣c は Cr 級,c(0)=p}/∼
\{ c : (-\varepsilon,\varepsilon) \to M \mid c \ \text{は} \ C^r \ \text{級}, c(0)=p \} / \sim
{c:(−ε,ε)→M∣c は Cr 級,c(0)=p}/∼
と定義する。
接ベクトル空間の元を接ベクトルという。
以下，曲線 ccc から定まる接ベクトルを [c][c][c] と書く。（同値類による区別のため）
方向微分を ppp を通る曲線により解釈した定義です。

              その同値類は何？
            
「点 ppp 周りで定義された曲線 → 接ベクトル」と定めている……ように思えて，謎の同値類での商を取っていますね。この同値関係はどういうモチベーションで設定しているのでしょうか。
ppp の近くで一致するものの，全体としては異なる曲線 c,c′c,c'c,c′ を考えてみましょう。それぞれが定める接ベクトルは一致します。
「点 ppp の周りで定義された曲線」という情報では，重複が発生してしまうのですね。
座標近傍を用いた考察接ベクトル空間がどのような構造であるか確かめるため，あえて座標近傍を思い出して計算してみます。
p∈Mp \in Mp∈M の座標近傍 (U,ϕ,V)(U,\phi , V)(U,ϕ,V) を固定します。特に VVV の座標を (x1,x2,⋯ ,xm)(x_1, x_2, \cdots , x_m)(x1​,x2​,⋯,xm​) としましょう。
ppp の近傍で定義された CrC^rCr 級写像 f:M→Rf : M \to \mathbb{R}f:M→R を取ります。
f∘c=(f∘ϕ−1)∘(ϕ∘c)
f \circ c = (f \circ \phi^{-1}) \circ (\phi \circ c)
f∘c=(f∘ϕ−1)∘(ϕ∘c)
と分解すると，ユークリッド空間とユークリッド空間の間の写像の合成と見なすことができます。ここで，chain rule を用いると ddt(f∘c)\dfrac{d}{dt} (f \circ c)dtd​(f∘c) が座標近傍を用いて記述することができるのです。
ddt(f∘c)(t)∣t=0=∑i=1m∂(f∘ϕ−1)∂xi(ϕ(p)){ddt(xi∘c(t))∣t=0}
\left. \dfrac{d}{dt} (f \circ c) (t) \right|_{t=0} = \sum_{i=1}^m \dfrac{\partial (f \circ \phi^{-1})}{\partial x_i} (\phi(p)) \left\{ \left. \dfrac{d}{dt} (x_i \circ c(t)) \right|_{t=0} \right\}
dtd​(f∘c)(t)∣∣​t=0​=i=1∑m​∂xi​∂(f∘ϕ−1)​(ϕ(p)){dtd​(xi​∘c(t))∣∣​t=0​}
と表すことができます。
簡単のために
∂(f∘ϕ−1)∂xi(ϕ(p))=∂f∂xi(p)
\dfrac{\partial (f \circ \phi^{-1})}{\partial x_i} (\phi(p)) = \dfrac{\partial f}{\partial x_i} (p)
∂xi​∂(f∘ϕ−1)​(ϕ(p))=∂xi​∂f​(p)
とおきます。すると ccc における方向微分は，座標近傍 (U,ϕ,V)(U,\phi,V)(U,ϕ,V) を固定すると
f↦∑i=1m∂f∂xi(p)(ddt(xi∘c(t))∣t=0)
f \mapsto \sum_{i=1}^m \dfrac{\partial f}{\partial x_i} (p) \left( \left. \dfrac{d}{dt} (x_i \circ c(t)) \right|_{t=0}\right) 
f↦i=1∑m​∂xi​∂f​(p)(dtd​(xi​∘c(t))∣∣​t=0​)
という写像だとみなすことができます。

接ベクトル空間の局所的な表示

局所的な表示
多様体 MMM について，p∈Mp \in Mp∈M の座標近傍 (U,ϕ,V)(U,\phi , V)(U,ϕ,V) を固定する。
p∈Mp \in Mp∈M における接ベクトルは，p∈Mp \in Mp∈M の座標近傍 (U,ϕ,V,(x1,⋯ ,xm))(U,\phi , V, (x_1, \cdots , x_m))(U,ϕ,V,(x1​,⋯,xm​)) について，
∑i=1mai(∂∂xi)p
\sum_{i=1}^m a_i \left( \dfrac{\partial}{\partial x_i} \right)_p  
i=1∑m​ai​(∂xi​∂​)p​
（a1,⋯ ,am∈Ca_1 , \cdots , a_m \in \mathbb{C}a1​,⋯,am​∈C）と表される微分演算子と表されます。
※ 微分演算子として (∂∂xi)pf:=∂f∂xi(p)\left( \dfrac{\partial}{\partial x_i} \right)_p f := \dfrac{\partial f}{\partial x_i} (p)(∂xi​∂​)p​f:=∂xi​∂f​(p) と定めている
定義1との関係定義1では，p∈Mp \in Mp∈M 近傍の曲線 ccc によって接ベクトルを定義しました。この ccc から定義2の微分演算子を定めることができます。
実際，座標近傍について
ai=ddt(xi∘c(t))∣t=0
a_i = \left. \dfrac{d}{dt} (x_i \circ c(t)) \right|_{t=0}
ai​=dtd​(xi​∘c(t))∣∣​t=0​
と定めればよいです。
そのため，{∂∂xi}\left\{ \dfrac{\partial}{\partial x_i} \right\}{∂xi​∂​} を「基底」として，それらの線型結合として表される微分作用素を接ベクトルと思えばよいのです。
座標近傍の取り換え先ほどの表示は，座標近傍に依存した表示となっていました。
多様体の定義を通して，特定の座標近傍を用いた表示を他の座標近傍を用いた表示に変換することができます。よって，上述の定義で問題ないのです。
p∈Mp \in Mp∈M の他の座標近傍 (U′,ϕ′,V′,(y1,⋯ ,ym))(U',\phi ', V', (y_1, \cdots , y_m))(U′,ϕ′,V′,(y1​,⋯,ym​)) を任意にとります。
このとき，多様体の定義から Rm\mathbb{R}^mRm における微分同相
ϕ′∘ϕ−1:ϕ(U∩U′)→ϕ′(U∩U′)
{\phi '} \circ \phi^{-1} : \phi (U \cap U') \to \phi ' (U \cap U')
ϕ′∘ϕ−1:ϕ(U∩U′)→ϕ′(U∩U′)
が存在します。これは
(y1y2⋮ym)=ϕ′∘ϕ−1(x1x2⋮xm)
\begin{pmatrix}
y_1 \\ y_2 \\ \vdots \\ y_m
\end{pmatrix} = 
\phi ' \circ \phi^{-1} 
\begin{pmatrix}
x_1 \\ x_2 \\ \vdots \\ x_m
\end{pmatrix} 
⎝⎛​y1​y2​⋮ym​​⎠⎞​=ϕ′∘ϕ−1⎝⎛​x1​x2​⋮xm​​⎠⎞​
という座標変換として表現されます。
よって，偏微分を用いて
(∂∂xi)p=∑j=1m∂yj∂xi(∂∂yj)p
\left( \dfrac{\partial}{\partial x_i} \right)_p =
\sum_{j=1}^m \dfrac{\partial y_j}{\partial x_i}
\left( \dfrac{\partial}{\partial y_j} \right)_p 
(∂xi​∂​)p​=j=1∑m​∂xi​∂yj​​(∂yj​∂​)p​
という変換が得られます。特にこの変換行列はヤコビアンになっています。

ベクトル空間の構造と次元

接ベクトル空間には，その名前の通りベクトル空間の構造が入ります。

定理

接ベクトル空間は，ベクトル空間の構造を持つ。

定理

$n$ 次元多様体 $M$ について，任意の点 $p \in M$ において接ベクトル空間 $T_p M$ のベクトル空間としての次元は $n$ になる。

まず $T_p M$ と $\mathbb{R}^n$ との間に全単射があることを証明します。

証明

写像の構成

$p \in M$ の座標近傍 $(U, \phi , V)$ を固定する。

接ベクトルの局所的な表示 $\begin{array}{cccc} \psi : & T_p M & \to & \mathbb{R}^m\\ & [c] &\mapsto & \begin{pmatrix} \left. \dfrac{d}{dt} (x_i \circ c(t)) \right|_{t=0} \end{pmatrix} \end{array}$ という対応を考える。これはベクトル空間としての同型であることを示せばよい。

単射性

$[c],[c'] \in T_p M$ は各 $i$ について $\left. \dfrac{d}{dt} (x_i \circ c(t)) \right|_{t=0} = \left. \dfrac{d}{dt} (x_i \circ c'(t)) \right|_{t=0}$ を満たすものとする。

任意の $p$ の近傍で定義された $f: M \to \mathbb{R}$ に辺々適用し chain rule を用いて整理すると $\left. \dfrac{d}{dt} (f \circ c) \right|_{t=0} = \left. \dfrac{d}{dt} (f \circ c') \right|_{t=0}$ となるため2つの元は接ベクトルとして等しい。

全射性

座標近傍 $(U,\phi,V)$ で $\sum_{i=1}^m a_i \left( \dfrac{\partial}{\partial x_i} \right)_p$ と表される接ベクトルを考える。

$\phi (p) \in \mathbb{R}^m$ を $\phi (p) = q = \begin{pmatrix} q_1\\\vdots \\ q_m \end{pmatrix}$ とおく。

このとき， $c(t) = \phi^{-1} \begin{pmatrix} q_1 + a_1t\\ \vdots\\ q_m + a_m t \end{pmatrix}$ と定めることで $[c] \in T_p M$ を得る。

上で示した同型を通して $T_p M$ にベクトル空間の構造を定める。

和やスカラーの構造，零元について確認しましょう。

和

$v,v' \in T_p M$ について， $p$ の座標近傍 $(U,\phi , V)$ でそれぞれ $v : \sum_{i=1}^m a_i \left( \dfrac{\partial}{\partial x_i} \right)_p\\ v' : \sum_{i=1}^m b_i \left( \dfrac{\partial}{\partial x_i} \right)_p$ と表されることにする。

このとき， $v+v'$ を座標近傍 $(U, \phi ,V)$ で $\sum_{i=1}^m (a_i+b_i) \left( \dfrac{\partial}{\partial x_i} \right)_p$ と表される元と定める。実際に前節からこのような元を取ることができる。

また座標近傍を固定して $v+v'$ を定義したが，ヤコビアンを通した座標変換により，他の座標近傍を用いて定義しても同じ元を与えていることが分かる。（well-defined 性）

スカラー倍

和と同様に定義する。

零元

零元は，恒等的に $p$ となる写像 $c(t) = p \ (- \varepsilon < t < \varepsilon)$ から得られる元の同値類 $[c]$ となる。

以上より $T_p M$ は $\mathbb{R}^m$ と同型なベクトル空間であることが分かります。よって，次元は $m$ となり多様体の次元と一致します。

特に接ベクトルの元を局所的な表示で表した場合，接ベクトル空間の基底として $\left\{ \left( \dfrac{\partial}{\partial x_i} \right)_p \right\}$ を取ることができます。

余接ベクトル空間

元の表現接ベクトル空間の双対ベクトル空間を余接ベクトル空間といいます。
線型汎関数と双対ベクトル空間
記号としては
TpM∗=Hom(TpM,R)
T_p M^{\ast} = \mathrm{Hom} (T_p M , \mathbb{R})
Tp​M∗=Hom(Tp​M,R)
と書きます。
余接ベクトル空間の元
ppp の近傍で定義された C1C^1C1 級関数 f:M→Rf : M \to \mathbb{R}f:M→R を考える。
(df)p(df)_p(df)p​ を
(df)p:[c]↦ddtf(c(t))∣t=0
(df)_p : [c] \mapsto \left. \dfrac{d}{dt} f(c(t)) \right|_{t=0}
(df)p​:[c]↦dtd​f(c(t))∣∣​t=0​
と定義することで (df)p∈TpM∗(df)_p \in T_p M^{\ast}(df)p​∈Tp​M∗ となる。
実際，任意の TpM∗T_p M^{\ast}Tp​M∗ の元はこのように記述することができます。
局所的な表示と基底まず p∈Mp \in Mp∈M の座標近傍 (U,ϕ,V)(U, \phi , V)(U,ϕ,V) を取ります。
座標 xix_ixi​ を ppp の近傍で定義された C1C^1C1 級関数とみなします。
具体的には x∈Mx \in Mx∈M に対して xi(x)x_i (x)xi​(x) を「ϕ(x)\phi (x)ϕ(x) の iii 番目」により定めることで C1C^1C1 級関数とみなします。
余接ベクトル空間の性質
∂xj∂xi=δij\dfrac{\partial x_j}{\partial x_i}  = \delta_{ij}∂xi​∂xj​​=δij​（分子は前述した関数としての xjx_jxj​，分母は座標近傍の座標としての xix_ixi​）
{(dxi)p}\{ (dx_i)_p \}{(dxi​)p​} は TpM∗T_p M^{\ast}Tp​M∗ の基底である。特に {(∂∂xi)p}\left\{ \left( \dfrac{\partial}{\partial x_i} \right)_p \right\}{(∂xi​∂​)p​} の双対基底である。
(df)p(df)_p(df)p​ は
(df)p=∑i=1m(dfdxi)(p)(dxi)p
(df)_p = \sum_{i=1}^m \left( \dfrac{df}{dx_i} \right) (p) (dx_i)_p 
(df)p​=i=1∑m​(dxi​df​)(p)(dxi​)p​
と記述できる。

接ベクトル空間のもう1つの定義

ここまでは曲線を介した定義を紹介してきました。

この節では曲線を介さない抽象的な定義を紹介し，それが等価であることを示します。

準備：余接ベクトルを通した別の視点

一般に（有限次元）ベクトル空間では，双対ベクトル空間の双対は元のベクトル空間となります。ゆえに接ベクトルは，余接ベクトル空間から $\mathbb{R}$ への線型写像とみなされます。

具体的に $v \in T_p M$ ， $(df)_p \in T_p M^{\ast}$ について $v(f) = (df)_p (v) \in \mathbb{R}$ と定義します。

このとき，積の微分公式から $v(fg) = v(f) g(p) + f(p) v(g)$ が成立します。

上記を参考に方向微分という概念を導入します。

方向微分

定義

$M$ は $C^r$ 級多様体とする。 $p \in M$ とする。

$p$ の近傍で定義された $C^{1}$ 級関数から $\mathbb{R}$ への線型写像であって，

$v(af+bg) = a v(f) + b v(g)$ （線型性）
$v(fg) = v(f) g(p) + f(p) v(g)$ （微分）

を満たす $v$ を $p$ の方向微分という。

※ $f,g$ は $p$ の近傍で定義された $C^{1}$ 級関数とする。

実は方向微分の集合を接ベクトル空間と定義することができます。

定理

方向微分 $v$ について，ある $v' \in T_p M$ が存在して，任意の $p$ の近傍で定義された $C^{1}$ 級関数 $f : M \to \mathbb{R}$ について $v(f) = v'(f)$ となる。

ゆえに方向微分を接ベクトルとみなすことができる。

次回は多様体の写像から誘導される接ベクトル空間の間の線型写像について解説します。