多様体入門3~多様体の間の写像の可微分性
更新
を多様体とし,座標近傍系をそれぞれ , とする。
多様体の間の連続関数 が 級であるとは,
- 任意の , に対して (これは の開集合から の開集合への連続関数になる)が 級である
ことをいう。
多様体入門1で「多様体は微分ができる空間」と紹介しました。今回はそんな多様体の間の写像の とはなにか解説していきます。
イメージ図
イメージ図
定義式だけではわかりにくいので絵で理解を深めましょう。
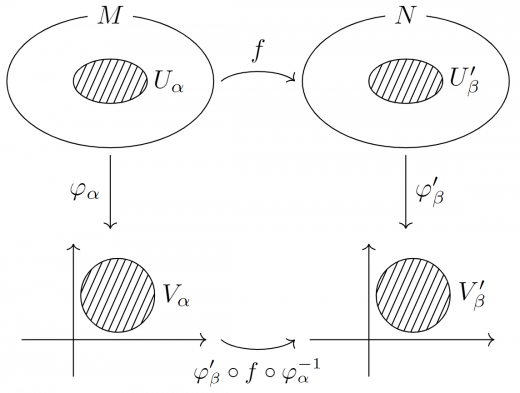
ポイントとしてはアトラスまで指定した上で が定義されているところです。
判定法
判定法
そもそも 関数は(実数上で)どう定義されていたかを思い出してみましょう。
で定義された関数 が 上で 級であるとは,任意の で が 級であることをいう。
……ということは多様体の 級の定義も各点での 級と等価であるべきですね。実は次の定理が成り立ちます。
級多様体の間の連続関数 が 級であることと次の条件は同値である。
- 任意の に対して,ある , が次を満たすように存在する。
- , かつ は の近傍で 級である。
が 級であれば,もちろん条件を満たす。
逆に条件を満たすと仮定する。
, を任意にとる。 が 級であることを示すことになる。
このとき条件から任意の について,ある , があって である。
, は 級多様体であるため,, はどちらも 級同相写像である。
よって の近傍で は 級である。
の任意の点上で同様の議論ができるため, は 全体で 級である。こうして示された。
多様体の微分同相性
多様体の微分同相性
多様体の写像 が 級微分同相であるとは,ある 級写像 があって , となることをいう。
また,このとき と は 級微分同相であるという。
関連する定理
と は 級微分同相とする。()
このとき, と の次元は一致する。
極大アトラス
極大アトラス
の 性はアトラスに依存していました。
異なるアトラスが入った多様体 について,一番良いアトラスがどうなるのか考察していきます。
, をそれぞれ 級多様体 上のアトラスとする。
と が両立することを が 級微分同相であることと定義する。
このことは もまた のアトラスになることと同値である。
※ 「両立する」を「同値である」ということもある。
適当なアトラス と両立するアトラスをすべて集めてその合併を取ると,定義からそれもまたアトラスになります。このアトラスは非常に詳細な座標近郷を定めるため,ある意味で「一番いいアトラス」といえます。
を多様体 のアトラスとする。 と両立するアトラス全体の集合を とする。
このとき を極大アトラスという。
やや慣れない計算が必要ですが慣れましょう。











