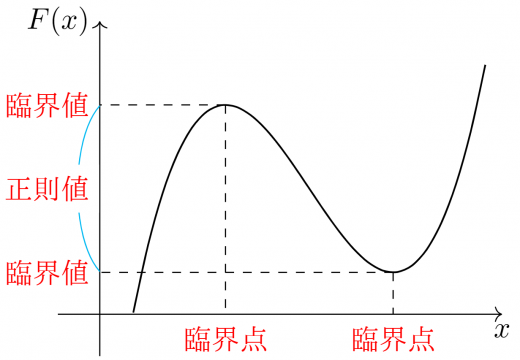
定義や定理だけでは分かりにくいので,実際に例を確認してみましょう。
多項式によって定まる多様体
臨界値の例題から……
例
x3+y3−3xy=1 は多様体になる。
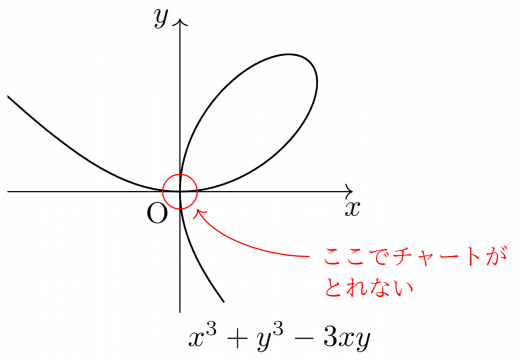
x3+y3−3xy=0 は多様体にならない。
多様体にならない方のグラフは下のようになります。
原点でグラフが交叉するため,そこでチャートを取ることができません。そのため多様体にはなれません。
他にも例
例
{x=y2xy+z=0
により定義される図形は多様体になる。
証明
F(x,y,z)=(x−y2,xy+z) とする。
(JF)(x,y,z)=⎝⎛∂x∂F1∂x∂F2∂y∂F1∂y∂F2∂z∂F1∂z∂F2⎠⎞=(1y−2yz01)
任意の (x,y,z) において rank (JF)(x,y,z)=2 となる。
よって,任意の (x,y,z)∈F−1(0) は正則値であるため,F−1(0) は多様体になる。
特別な行列の集合が成す多様体
特殊線型群
例
特殊線型群
SLn(R)={A∈Mn(R)∣detA=1}
は多様体になる。
ヤコビアンの計算をどうやるのかがポイントです。
証明
Mn(R) の座標を (xij) で表す。
A=(aij) と表記する。
∂xij∂detA=dtddet⎝⎛a11⋮ai1⋮an1⋯⋯⋯a1j⋮aij+t⋮anj⋯⋯⋯a1n⋮ain⋮ann⎠⎞∣∣t=0=det⎝⎛a11⋮ai1⋮an1⋯⋯⋯0⋮1⋮0⋯⋯⋯a1n⋮ain⋮ann⎠⎞=Aの第(i,j)余因子行列式
となる。
det のヤコビアン (Jdet)A は,A の第 (i,j) 余因子行列式を並べたものになる。
今,A∈SLn(R) の行列式は 1 であるため,少なくとも1つの余因子行列は 0 にならない。
ゆえに rank (Jdet)M=1 である。
det は多項式の形で表されるため C∞ 級である。
こうして SLn(R) は C∞ 級多様体になる。
※ ちょっと分かりにくいですが,この場合のヤコビアンは
(∂x11∂det∂x12∂det⋯∂xnn∂det)
と横一列に 1×n2 行列になります。
直交群
例
直交群
O(n)={A∈Mn(R)∣tAA=In}
は多様体になる。
証明
n×n 対称行列の集合を Symn(R) で表す。
F:Mn(R)→Symn(R) を
F(A)=tAA
とする。(tA は A の転置行列)ここで F は C∞ 級である。
O(n)=F−1(In) となる。
ヤコビアン (JF)A:Mn(R)→Symn(R) を計算する。
(JF)A(X)=dtdt(A+tX)(A+tX)∣∣t=0=tXA+tAX
In∈Symn(R) は正則値であることを示す。
A∈F−1(In) に対して (JF)A が全射であることを示せばよい。
Y∈Symn(R) を任意に取る。ここで X=21AY とすると
(JF)A(X)=21tYtAA+21tAAY=21tY+21Y=Y
となるため,(JF)A は全射である。
こうして In は正則値であることが分かった。
よって O(n) は C∞ 級多様体となる。
ヤコビアンが全射であることをダイレクトに示す方法で確認しました。方法として覚えておいて損はないです。