写像・単射・全射
写像の意味と,それにまつわる概念である全射・単射について紹介します。
写像のことを学習する際は,集合の記号について押さえておく必要があります。 集合の記号については,集合の記号の意味まとめ もぜひご覧ください。
写像
写像
写像は,中学数学で習う関数と基本的には同じ意味です。まずは,写像をきちんと定義しましょう。
集合 がある。任意の に対して, の要素を1つ返すような対応 を から への 写像 という。またこのとき と書くことがある。

- に対する出力(返り値,結果,対応先)を と書きます。
- を始域(定義域)と言います。入力として許される範囲です。
- を終域と言います。
に対して と定めると, は写像になる。
に対して と定義する。これは写像にならない。
実際, で となる。
であった。この は1つの入力に対して複数の出力を持ち得るため,写像ではない。
像(値域)と逆像の定義
次に,像(値域)と逆像についての定義を説明します。
-
に対して, の像 を以下で定義する:
-
に対して, の逆像 を以下で定義する:
を と定義すると, は2の倍数全体の集合になる。
集合 を考えます。, という写像があるとき, の合成 が にて定義されます。つまり, は,任意の に対して を返す写像です。
単射と全射,全単射
単射と全射,全単射
単射・全射(上からの写像)の定義
写像 について考える。
-
とする。 であるとき, は 単射 であるという。
-
任意の に対して,ある があって となるとき, は 全射 であるという。
図による単射・全射のイメージは下図のようになります。

単射と全射のイメージは 関数方程式の解き方のコツ〜全射と単射〜 に詳しく書いてあります。
全射では,始域の像が終域全体になります。このことから,全射のことを「上への写像」と呼ぶこともあります。
全単射(上への写像)の定義
単射・全射に引き続き,全単射の定義も重要です。
- 写像 が単射かつ全射であるとき, を 全単射 であるという。このとき, と は 1対1に対応する という。
図による全単射のイメージは下図のようになります。
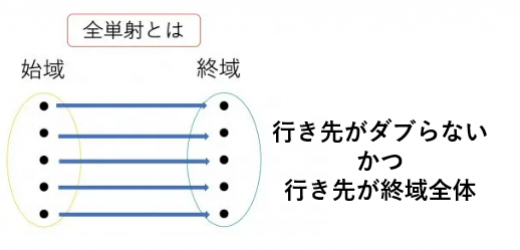
が全単射なら, の元 を1つ取ったら により がただ1つ定まり, の元 を取ったら, なる の元 がただ1つ定まります。まさに1対1です。
-
を とすると,これは単射である。
-
を とおくと,これは全射である。なお実数 に対して は を越えない最小の整数を意味する。
-
を とすると,これは全単射である。
恒等写像と逆写像
恒等写像と逆写像
恒等写像
全ての元をそっくり同じものに写す操作はもちろん写像の定義を満たします。このような写像を恒等写像といいます。
写像 が,任意の に対して を満たすとき, を 恒等写像 という。このとき と書くことがある。
逆写像
を と定義しましょう。具体的に計算をしてみましょう。
さてここで とすると
となり, と逆向きに数を写すことがわかります。
このような写像を逆写像といいます。
写像 に対して,写像 で , なるものが存在するとき, を の 逆写像 という。このとき と書く。
- を とおくと, が逆写像となる。
が逆写像を持つ必要十分条件として次が知られています。
写像 が逆写像を持つことと が全単射であることは同値である。
逆写像を持つ 全単射
を の逆写像とする。
-
単射
は を満たすものとする。
は逆写像であるため, である。よって は単射である。 -
全射
を任意に取る。このとき で である。よって は全射である。
逆写像を持つ 全単射
は全単射であるとする。
は全射であるため,任意の に対して,ある が存在して となる。このような は一意に定まる。実際 もまた であるとすると, であるが,単射性より である。
よって に対して と定めると は写像になる。
作り方から , であるため, は逆写像である。
写像は数学をする上で避けては通れません。様々な例と共に身につけましょう。











