重複順列の意味と例題

重複順列の公式で $n=3,r=2$ の場合なので $3^2=9$ 通り。

ちなみにすべて列挙すると， $$aa,ab,ac,ba,bb,bc,ca,cb,cc$$ の $9$ 通り。

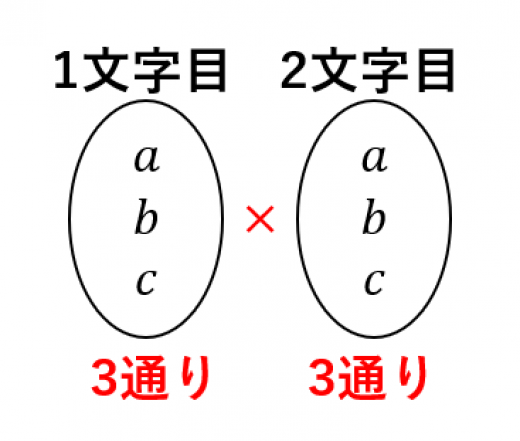
• 1個目に $a,b,c$ のどれを選ぶかで $3$ 通り
• そのそれぞれについて，2個目に $a,b,c$ のどれを選ぶかで $3$ 通り

結局 $3\times 3=9$ 通り。

重複順列の公式で $n=9,r=3$ の場合なので $9^3=729$ 通り。

• 1桁目に $1$～$9$ のどれを選ぶかで $9$ 通り
• そのそれぞれについて，2桁目に $1$～$9$ のどれを選ぶかで $9$ 通り
• そのそれぞれについて，3桁目に $1$～$9$ のどれを選ぶかで $9$ 通り

結局 $9\times 9\times 9=729$ 通り。

• 1番目に $n$ 種類のどれを選ぶかで $n$ 通り
• そのそれぞれに対して，2番目に $n$ 種類のどれを選ぶかで $n$ 通り

ここまでで $n^2$ 通り

• そのそれぞれに対して，3番目に $n$ 種類のどれを選ぶかで $n$ 通り

ここまでで $n^3$ 通り

これを $r$ 番目まで繰り返すと $n^r$ 通りになる。