円順列の公式と2通りの考え方
更新
異なる 個のものを円形に並べる方法の総数は 通り
円順列について,意味・公式・2通りの考え方・例題を解説します。
円順列の意味
円順列の意味
- いくつかのものを一列に並べる方法のことを順列と言います。例えば, を並べる順列は図のように 通りあります。
- また,いくつかのものを円形に並べる方法のことを円順列と言います。
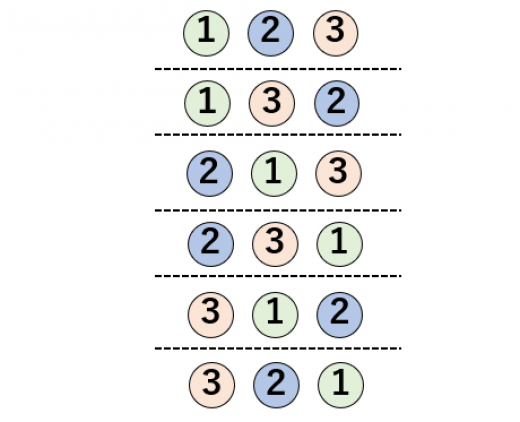
- 円順列では回転して一致する並べ方は同じと考えます。例えば, を円形に並べる方法は 通りありそうですが「回転して一致する並べ方は同じ」と考えるので 通りになります。
さっそくですが,円順列の公式を使ってみましょう。
5人が円形のテーブルに座るとき,その座り方の総数は何通りであるか。
5人を「円形に並べる」ので円順列です。
円順列の公式 で とすると,答えは
通り
円順列の公式の証明・考え方
円順列の公式の証明・考え方
円順列の公式 を2通りの考え方で証明してみます。
考え方1
円順列では,回転させて一致するものは同じ並べ方とみなします。
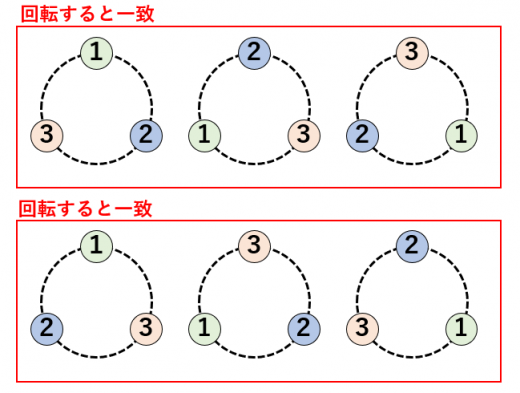
異なる 個のものを円形に並べるとき,それぞれ 通りが「同じ並べ方」になる。
例えば, のとき,図のような つの並べ方は回転させて一致するので「同じ並べ方」である。
以上をふまえて,
- 個のものをとりあえず並べる順列の数は 通りである。→順列と組合せの違いと例題
- ただし,それぞれについて「同じ並べ方」が 通りカウントされてしまうので, で割る必要がある。
つまり,円順列の数は 通りとなる。
考え方2
1つを固定して考えるという方法もあります。1つを固定することで「回転」を考えなくてよくなります。
個のものを円形に並べるとき,1つを固定して考えると,残り 個を並べる順列の個数に等しい。よって
通りになる。
※円形のテーブルに自分が座っているところを想像してみるとよいです。残り 人の並べ方が 通りです。
円順列の例題
円順列の例題
続いて,もう少し複雑な円順列の例題です。並べるものの中に同じものを含む問題です。
大人4人と子供4人が円形のテーブルの周りに座るときに,子供と大人が交互に並ぶ並び方の総数は何通りであるか。
先に大人を円順列で並べておいて,その間に子供を配置します。
まず,大人4人が円形に並ぶ並び方は円順列の公式より
次に子供の並び方は,大人の間に子供を入れるように並べればよいから
よって,求める総数は
次は,もう少し複雑な処理が必要な円順列についての例題です。
男子2人と女子4人が輪を作って並ぶとき
(1)男子2人が隣り合う場合
(2)男子2人が向かい合う場合
はそれぞれ何通りか。
(1)通常の順列のときと同様に男子2人をひとまとまりに考える。まず,男子2人の並び方は2通り。
また,ひとまとまりの男子と女子4人の円順列は よって,求める総数は
(2)まず,男子2人が向かい合って座る座り方は1通り。
次に,女子の並び方は,向かい合っている男子が固定されているため一列に並べる順列として考えると
-
最短で得点力を上げる!高校数学の問題集〈典型250問〉 の問題141では,他の類題と計算ミスを減らすコツを紹介しています。
-
さらに複雑な問題については,同じものを含む円順列の裏技公式を参照してください。
円順列と数珠順列
円順列と数珠順列
円順列に似たものとして数珠順列というものもあります。
- 円順列では「回転して一致するものは同じ並べ方」とみなしました。
- 数珠順列では「回転または裏返しで一致するものは同じ並べ方」とみなします。図のような2つの並べ方は「同じ」とみなします。

- 円順列の場合に加えて,それぞれ2つの並べ方が「同じ」なので数珠順列については以下の公式が成立します。
異なる 個のものを数珠順列で並べるとき,並べ方の総数は
数珠順列についての例題を解いてみましょう。
赤,青,黄,緑,黒の玉で数珠を作るとき,作り方の総数は何通りあるか。
「回転または裏返しで一致するものは同じ数珠なので同じ作り方とみなす」ので,数珠順列の問題である。
異なる5個のものの数珠順列であるから
次は並べるものに区別できないものがある場合の例題です。
赤玉2個,青玉2個,黒玉1個の合計5個の玉がある。ここで,次の問に答えよ。
(1) これらを円形に並べる方法は何通りあるか。
(2) これらに糸を通して腕輪を作る方法は何通りあるか。
(1) 1個しかない黒玉を固定して考えると,これらの玉を円形に並べる総数は,赤玉2個,青玉2個を一列に並べる方法の数に等しいから
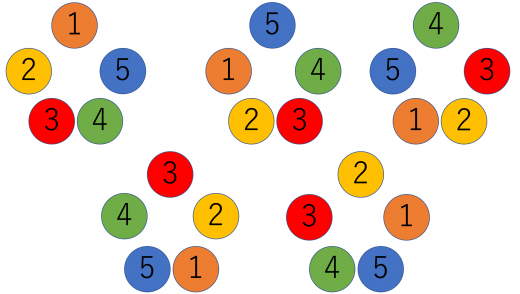
(2) (1)で求めた円順列のうち,裏返しても変わらないものは図の2通り。
 よって,腕輪の作り方は
よって,腕輪の作り方は
円順列の考え方のまとめ
円順列の考え方のまとめ
- 公式 を当てはめるというよりも「回転して一致するものは同じ」「1つを固定して考える」という考え方の理解が重要です。
- 円順列に同じものが含まれるときは,どこに円順列の考え方を用いるか注意しましょう。
円順列・数珠順列あたりの話題は公式丸暗記で乗り切るのは厳しいです。しっかり考え方を理解しましょう。









