重複組合せの公式と例題（玉，整数解の個数）

重複組合せ，つまり「重複を許して」選ぶ組合せが何通りあるかを考えます。

重複組合せの例題です。

• 青，赤，黒それぞれ何回でも使えます（重複を許す）。
• 順番は区別しません（順列ではなく組合せ）。例えば「青青赤青」と「青青青赤」は区別せず同じパターンとみなします。

もれなくダブリなく数えるのは大変ですね…。

実は，重複組合せは以下の公式で計算できます。

$n$ 種類のものから重複を許して $r$ 個選ぶ場合の数は ${}_{n+r-1}\mathrm{C}_r$

15通り列挙するより簡単です！

→高校数学の問題集　～最短で得点力を上げるために～のT50も参照してください。

まずは，例題1の場合でなぜ ${}_{6}\mathrm{C}_4$ になるか説明します。

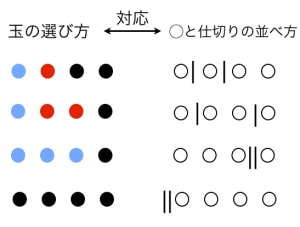
「三種類の玉から4つ選ぶ方法」と「◯4つと仕切り2つを一列に並べる方法」は図のように1対1に対応するので，求める場合の数は $\dfrac{6!}{4!2!}={}_6\mathrm{C}_4$ 通り。

公式の証明は，上の例を一般化するだけです。

$n$ 種類のものから重複を許して $r$ 個選ぶ場合の数を ${}_n\mathrm{H}_r$ と書くことがあります。

重複組合せの公式より ${}_n\mathrm{H}_r={}_{n+r-1}\mathrm{C}_r$です。

ただし，重複組合せの問題はさきほど述べた「仕切りの考え方」で必ず解けます。そのため，${}_n\mathrm{H}_r$ という記号や，重複組合せの公式を覚える必要は全くありません。

むしろ，重複組合せの公式は仕切りの考え方を使って証明するので，仕切りの考え方を覚えておく方が重要です。

解答1（重要）：最初に三種類の玉を1つずつ取ってくる。残り二つの玉の選び方を数えればよい（＊）。それはさきほどと同様に，「玉2つと仕切り2つを一列に並べる方法」の数に等しいので $\dfrac{4!}{2!2!}=6$ 通り。

解答2：（＊）までは解答1と同じ。重複組合せの公式より ${}_3\mathrm{H}_2={}_{4}\mathrm{C}_2=6$ 通り。

解答3：これくらいなら全部列挙して検算するべきですね。

（青，赤，黒）＝ $(2,2,1),(2,1,2),(1,2,2),(3,1,1),(1,3,1),(1,1,3)$ の $6$ 通り。

重複組合せの応用として整数解の個数を求める問題は頻出です。玉の場合と全く同じ考え方でOKです。

• 重複組合せの公式よりも仕切りの考え方が重要
• 「全てを1つ以上選ぶ」パターンの場合，予め1つずつ分配しておく
• 整数解の個数も重複組合せで解けることがある

Tag:数学Aの教科書に載っている公式の解説一覧