図形の対称移動・グラフの対称移動

線対称移動とは，ある直線に関して折り返す移動です。

線対称移動の性質として「対称軸が，対応する点どうしを結んだ線分の垂直二等分線になる」が挙げられます。

まずは点の対称移動を考えます。点 $A$ を，軸を中心に折り返して点 $A'$ に移すことを考えます。このとき，$A$ と $A'$ を結んだ線分の垂直二等分線が「軸」になっています。

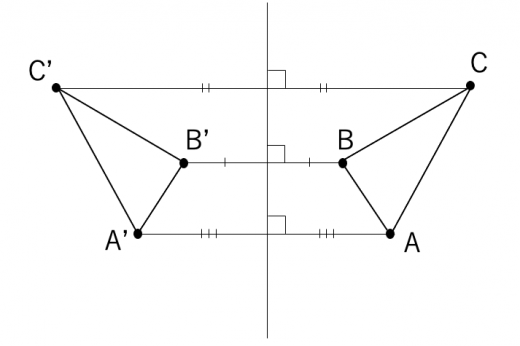
次に，図形の線対称移動を考えます。三角形 $ABC$ を線対称移動させてみましょう。

まず，頂点 $A,B,C$ を軸を中心に折り返して点 $A',B',C'$ に移します。このとき，$A$ と $A'$ を結んだ線分の垂直二等分線，$B$ と $B'$ を結んだ線分の垂直二等分線，$C$ と $C'$ を結んだ線分の垂直二等分線が全て軸に一致します。移動後の点 $A',B',C'$ を結んで三角形を作ると，三角形 $ABC$ を線対称移動させた三角形を作ることができます。

いろいろな線分を軸として考えて，対称移動したらどうなるかを考えてみましょう。

線分 $BF$ を軸とすれば，$1$ の三角形を対称移動すると $4$ と重なります。線分 $DH$ を軸とすれば，$1$ の三角形を対称移動すると $8$ と重なります。

$2$ も答えになるのではないかと思った方もいるかもしれませんが，もう一度よく考えてみてください。$H$ を $AE$ を軸に対称移動させても，$B$ とは重なりませんね。

よって答えは $4,8$ と重なります。

点対称移動を説明するにあたり、まずは回転移動について確認します。回転移動とは「図形や点が大きさや形を変えずに，中心と呼ばれるある点を基準に，ある角度回転して移動すること」を言います。

回転移動には「ある点と，その点に対応する回転した後の点において，それぞれの点から回転の中心までの距離は等しく，またどの点も中心周りを同じ角度だけ回転する」という性質があります。

そして，特に回転角が $180^{\circ}$ である回転移動のことを点対称移動と言います。

点対称移動には「回転の中心が，対応する点どうしを結んだ線分の中点になる」という性質があります。

例として，三角形を点対称移動させたものを下に示します。

余談ですが，座標平面上で回転移動させたいときは，高校で習う複素数を使うと，単純な掛け算で回転先の座標を知ることができます。→複素数平面における極形式と回転

ここまで，図形の線対称移動，点対称移動について考えました。次は，座標平面上における線対称移動，点対称移動を考えてみます。

まず，ある点 $(x,y)$ の線対称移動，点対称移動を考えます。

ある点 $(x,y)$ を $x$ 軸に関して（$x$ 軸を対称の軸として）線対称移動させることを考えると，対応するのは $(x, -y)$ であることがわかります（図を描いてみると一目瞭然です）。

さらに，$(x,y)$ を $y$ 軸に関して線対称移動させることを考えると，対応するのは $(-x, y)$ であることもわかります。

つまり，座標平面上において，1点を $x,y$ 軸を対称の軸として線対称移動させることは，成分の符号を変えることに対応します。とてもラクですね。

また，$(x,y)$ を原点 $O$ に関して（$O$ を回転の中心として）点対称移動させることを考えると，対応するのは $(-x, -y)$ であることがわかります。

つまり，座標平面上において点を原点 $O$ を回転の中心として点対称移動させることも，成分の符号を変えることに対応します。

次に，グラフの対称移動を考えます。グラフは点の集合であることを考えると，グラフの対称移動というのは，全ての点一つずつをそれぞれ対称移動したものと考えることができます。

よって，一般に以下のようなことが言えます。

前節のまとめを利用します。関数 $y = f(x)$ のグラフを $x$ 軸に関して線対称移動させたものは $-y = f(x)$ に等しいので，$y = 2x^2 + x -4$ を $x$ 軸に関して対称移動させると $$\begin{aligned} &-y = 2x^2 + x -4\\ &\therefore y = -2x^2 - x +4 \end{aligned}$$ となります。同様に，$y$ 軸に関して対称移動させると $$\begin{aligned} &y = 2(-x)^2 + (-x) -4\\ &\therefore y = 2x^2 - x -4 \end{aligned}$$ となります。最後に，原点 $O$ に関して対称移動させると $$\begin{aligned} &-y = 2(-x)^2 + (-x) -4\\ &\therefore y = -2x^2 + x +4 \end{aligned}$$

各グラフの位置関係は以下の図のようになります。

緑の曲線は $y = 2x^2 + x -4$，赤の曲線は $y = -2x^2 - x +4$，灰色の曲線は $y = 2x^2 - x -4$，青色の曲線は $y = -2x^2 + x +4$ を表しています。