平面幾何の美しい定理4つ
更新
平面図形の美しい定理を4つ紹介します。
パップスの定理
パップスの定理
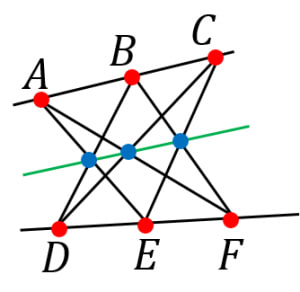
,, が同一直線上にある。
,, が同一直線上にある。
と の交点を
と の交点を
と の交点を
とするとき,,, は同一直線上にある。
メネラウスの定理を駆使することで証明できます。
ブリアンションの定理
ブリアンションの定理
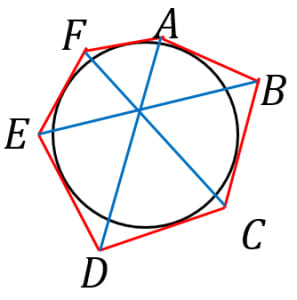
円に外接する六角形 について,三直線 ,, は一点で交わる。
より一般に,円を一般の二次曲線に拡張したバージョンもあります。
Brianchon’s theorem(英語サイト)ではブリアンションの定理を3行で証明しています。ただし,根軸・根心についての知識が必要です。→根軸の性質と根心の存在定理
パスカルの定理
パスカルの定理

六点 ~ が円上にある。
と の交点を
と の交点を
と の交点を
とするとき,,, は同一直線上にある。
図は の順に並んでいる場合ですが,別の順番でもOKです。
「円と六角形」という観点で見れば,ブリアンションの定理と似ていますね(実は,二つの定理は射影幾何における「双対」という関係にある)。
また,この図( の順番の図)はパップスの定理とも似ていますね。
ペンタグラムおける美しい定理
ペンタグラムおける美しい定理
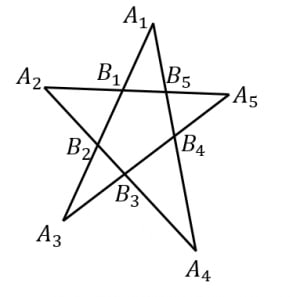
がペンタグラム(5つトゲを持つ星)のとき,
お星様の周りを一周する感じです。
(メネラウスの定理を用いた証明など,この定理の詳細はA Menelaus-Type Theorem for the Pentagramに載っています(読者の方に教えていただきました)。
パップスの定理の図を見ていると,あやとりを思い出します。











