空間内の格子点の数え上げ～京大特色2026第3問

$n$ を $-\dfrac{t}{a} \leqq n \leqq \dfrac{t}{a}$ を満たす整数として，$z = n$ での断面を考える。これを $V_n (t)$ とおく。

このとき，$V_n(t)$ は $$x^2 + y^2 \leqq t^2 - a^2n^2$$ である。この円盤上の格子点の個数を $M_n$ とおく。

このとき，対称性に注意すると $$N(t) = M_0 + 2 \sum_{n=1}^{\left\lfloor \frac{t}{a} \right\rfloor} M_n$$ である。

円盤の格子点の評価

各 $\mathrm{P} \in V_n (t)$ について，その点を中心とする辺の長さが $1$ の正方形の和集合を $S_n$ で表す。各正方形の面積は $1$ であるため，$S_n$ の面積は，$V_n$ の格子点の個数と一致することに注意する。

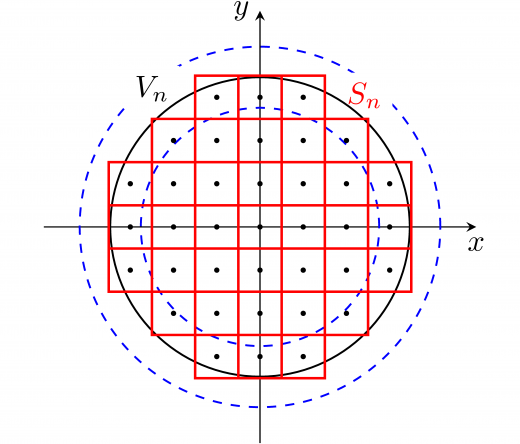
$S_n$ の点と格子点の距離は高々 $\dfrac{1}{\sqrt{2}}$ である。ゆえに $$D_1 : x^2+y^2 \leqq t^2-a^2n^2 +\dfrac{1}{2}\\ D_2 : x^2+y^2 \leqq t^2-a^2n^2 -\dfrac{1}{2}$$ とおくと $D_2 \subset S_n \subset D_1$ である。よって，面積を比較することで $$\pi \left( t^2-a^2n^2-\dfrac{1}{2} \right) \leqq M_n \leqq \pi \left( t^2-a^2n^2+\dfrac{1}{2} \right)$$ を得る。

各 $n$ について和を取り，辺々を $\pi$ で割ると $$\begin{aligned} &\left( t^2-\dfrac{1}{2} \right) \left(2\left\lfloor \frac{t}{a} \right\rfloor+1 \right)\\ &\quad - \dfrac{a^2}{3} \left\lfloor \frac{t}{a} \right\rfloor \left( \left\lfloor \frac{t}{a} \right\rfloor+1 \right) \left( 2\left\lfloor \frac{t}{a} \right\rfloor+1 \right)\\ &\leqq \dfrac{N(t)}{\pi}\\ &\leqq \left( t^2+\dfrac{1}{2} \right) \left(2\left\lfloor \frac{t}{a} \right\rfloor+1 \right)\\ &\quad - \dfrac{a^2}{3} \left\lfloor \frac{t}{a} \right\rfloor \left( \left\lfloor \frac{t}{a} \right\rfloor+1 \right) \left( 2\left\lfloor \frac{t}{a} \right\rfloor+1 \right) \end{aligned}$$ である。

$\displaystyle \lim_{t \to \infty} \dfrac{1}{t} \left\lfloor \frac{t}{a} \right\rfloor = \dfrac{1}{a}$ に注意すると $$\begin{aligned} &\lim_{t \to \infty} \dfrac{1}{t^3} \left\{ \left( t^2-\dfrac{1}{2} \right) \left(2\left\lfloor \frac{t}{a} \right\rfloor+1 \right) \right.\\ &\qquad\qquad \left. - \dfrac{a^2}{3} \left\lfloor \frac{t}{a} \right\rfloor \left( \left\lfloor \frac{t}{a} \right\rfloor+1 \right) \left( 2\left\lfloor \frac{t}{a} \right\rfloor+1 \right) \right\}\\ &= \dfrac{2}{a}-\dfrac{2}{3a} \\ &= \dfrac{4}{3a} \\ &\lim_{t \to \infty} \dfrac{1}{t^3} \left\{ \left( t^2+\dfrac{1}{2} \right) \left(2\left\lfloor \frac{t}{a} \right\rfloor+1 \right) \right.\\ &\qquad\qquad \left. - \dfrac{a^2}{3} \left\lfloor \frac{t}{a} \right\rfloor \left( \left\lfloor \frac{t}{a} \right\rfloor+1 \right) \left( 2\left\lfloor \frac{t}{a} \right\rfloor+1 \right) \right\}\\ &= \dfrac{2}{a}-\dfrac{2}{3a} \\ &= \dfrac{4}{3a} \end{aligned}$$ となる。よってはさみうちの原理から $$\lim_{t \to \infty} N(t) = \dfrac{4\pi}{3a}$$ を得る。