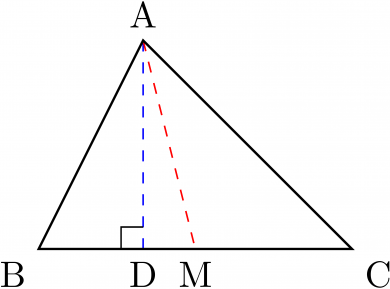
別の証明も見てみましょう。外接円の半径と三角形の面積公式
S=4Rabc
を用いて R の議論に置き換えて証明します。
パート1:式を簡単にする
以下,BC=a,CA=b,AB=c とおく。
△ABC の外接円の半径を R とすると
S=4Rabc
である。→ 外接円の半径と三角形の面積の関係(S=abc/4R)
これにより
916S2(a21+b21+c21)=9R21(a2b2+b2c2+c2a2)
である。
よって,示すべき不等式は
9R2(AP2+BP2+CP2)≧a2b2+b2c2+c2a2
である。
パート2:左辺の処理
ここでも 三角形の頂点からの距離の2乗和は重心で最小になることを活用して P を消します。
その後,重心と頂点の距離が
AG=92b+2c−a
と計算できることを用いて処理します。
実は R も同様に計算できます。
AG2+BG2+CG2 を a,b,c で表す。
三角形の頂点からの距離の2乗和は重心で最小になるため,
AP2+BP2+CP2≧AG2+BG2+CG2
である。(証明は前述の通り)
中線定理より
AB2+AC2=2(AM2+BM2)
である。整理することで
AM2=2AB2+AC2−2BM2=42b2+2c2−a2
を得る。
AMAG=32 であるため
AG2=92b2+2c2−a2
である。
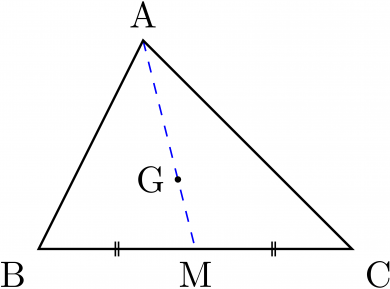
同様に BG,CG も計算できるため,
AG2+BG2+CG2=3a2+b2+c2
である。
よって
AP2+BP2+CP2≧3a2+b2+c2
を得る。
R の処理
一般に
9R2≧a2+b2+c2
が成立する。これを証明する。
△ABC の外心を O とおく。
3R2=AO2+BO2+CO2
である。
前述した事実を P=O で考えると
3R2=AO2+BO2+CO2≧AG2+BG2+CG2=3a2+b2+c2
が成り立つ。こうして題意は示された。
この事実はライプニッツの不等式と呼ばれます。詳しくは ライプニッツの不等式の3通りの証明 をご覧ください。
パート3:結論
上述したことから
9R2(AP2+BP2+CP2)≧31(a2+b2+c2)2
を得る。なお,等号成立は △ABC が正三角形かつ P が重心と一致するときである。
さて,
(a2+b2+c2)2−3(a2b2+b2c2+c2a2)=a4+b4+c4−a2b2−b2c2−c2a2=21{(a2−b2)2+(b2−c2)+(c2−a2)}≧0
(等号成立は a=b=c)であるため,
31(a2+b2+c2)2≧a2b2+b2c2+c2a2
を得る。
これらをまとめることにより,示すべき不等式
9R2(AP2+BP2+CP2)≧a2b2+b2c2+c2a2
が得られる。
三角形にまつわる色々な知識を総動員して証明ができました。計算幾何のおもしろい問題でしたね。