sin を繰り返し当てはめた関数の問題～京大特色2025第4問

更新 2024/11/28

京大特色2025 第4問

自然数 $n$ に対して，関数 $f_n (x)$ を次で帰納的に定める。

$\begin{aligned} f_1 (x) &= \sin x\\ f_n (x) &= \sin (f_{n-1} (x)) & (n = 2,3,4,\cdots) \end{aligned}$

また， $L$ を正の実数とし， $f_n (a) - \dfrac{a}{L} = 0$ を満たす実数の個数を $A_{L,n}$ とする。このとき，以下の設問に答えよ。

$L \leqq 1$ のとき， $\displaystyle \lim_{n \to \infty} A_{L,n}$ の値を求めよ。
$L > 1$ のとき， $\displaystyle \lim_{n \to \infty} A_{L,n}$ の値を求めよ。

ただし， $0$ 以上の実数からなる数列 $\{ a_n \}$ が，任意の $n$ に対して $a_{n+1} \leqq a_n$ を満たすとき，数列 $\{ a_n \}$ が収束することを用いてもよい。

この記事では京大特色2025の第4問を解説します。解析に関する問題です。答えをイメージしやすい問題ですが，丁寧な記述はハードだと言えます。さっそく挑戦していきましょう。

解答

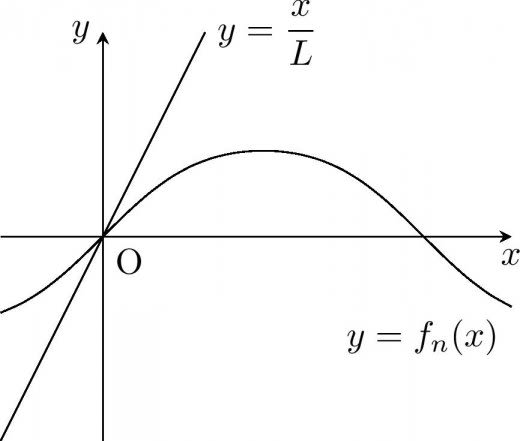
(1)証明
fn(x)=sin⁡(fn−1(x))
f_n (x) = \sin (f_{n-1} (x))
fn​(x)=sin(fn−1​(x))
帰納的に fn(0)=0f_n (0) = 0fn​(0)=0 であることを示す。
n=1n=1n=1 のとき fn(0)=sin⁡0=0f_n (0) = \sin 0 = 0fn​(0)=sin0=0 であるため，命題は成立する。
n=kn=kn=k のとき成立すると仮定する。このとき
fk+1(0)=sin⁡(fk(0))=sin⁡0=0
f_{k+1} (0) = \sin (f_{k} (0)) = \sin 0 =0
fk+1​(0)=sin(fk​(0))=sin0=0
より，仮定の元で n=k+1n=k+1n=k+1 の場合も成立する。
以上より fn(0)=0f_n (0) = 0fn​(0)=0 である．よって a=0a=0a=0 は題の方程式を満たす。
同様に帰納法で fn(x)f_n (x)fn​(x) は奇関数である。xL\dfrac{x}{L}Lx​ もまた奇関数であるため，x>0x > 0x>0 における解 aaa があれば −a-a−a も解で，逆も成立する。ゆえに x>0x > 0x>0 の場合を考えればよい。⋯(∗)\cdots (\ast)⋯(∗)
x>0x > 0x>0 で x>sin⁡xx > \sin xx>sinx である。よって
fn(x)=sin⁡(fn−1(x))<fn−1(x)
f_n (x) = \sin (f_{n-1} (x)) < f_{n-1} (x)
fn​(x)=sin(fn−1​(x))<fn−1​(x)
より，帰納的に fn(x)<x (x>0)f_n (x) < x \ (x > 0)fn​(x)<x (x>0) が成立する。
さて，L≦1L \leqq 1L≦1 より 1L≧1\dfrac{1}{L} \geqq 1L1​≧1 である。ゆえに x>0x > 0x>0 で
x<xL
x < \dfrac{x}{L}
x<Lx​
である。
以上より x>0x> 0x>0 で
fn(x)<x<xL
f_n (x) < x < \dfrac{x}{L}
fn​(x)<x<Lx​
であるため，
fn(a)−aL=0
f_n (a) - \dfrac{a}{L} = 0
fn​(a)−La​=0
を満たす正の実数は存在しない。(∗)(\ast)(∗) より方程式を満たす負の実数もまた存在しない。
こうして a=0a = 0a=0 のみが方程式を満たし，恒等的に AL,n=1A_{L,n} = 1AL,n​=1 となる。
ゆえに lim⁡n→∞AL,n=1\displaystyle \lim_{n \to \infty} A_{L,n} = 1n→∞lim​AL,n​=1 である。
イメージ図は次のようになります。
(2)方針の検討fn′(x)=cos⁡(fn−1(x))⋅fn−1′(x)
{f_n} '(x) = \cos (f_{n-1} (x)) \cdot {f_{n-1}} ' (x) 
fn​′(x)=cos(fn−1​(x))⋅fn−1​′(x)
より
fn′(0)=cos⁡0⋅fn−1′(0)
{f_n}'(0) = \cos 0 \cdot {f_{n-1}} ' (0)
fn​′(0)=cos0⋅fn−1​′(0)
であるため
fn′(0)=fn−1′(0)=⋯=1
{f_n}'(0) = {f_{n-1}}'(0) = \cdots = 1
fn​′(0)=fn−1​′(0)=⋯=1
です。ということは y=fn(x)y = f_n (x)y=fn​(x) は x=0x = 0x=0 の近傍で y=xy = xy=x と近似されます。一方 1L<1\dfrac{1}{L} < 1L1​<1 より，x=0x = 0x=0 の近傍で y=xLy = \dfrac{x}{L}y=Lx​ のほうが「下」にあることがイメージできます。
十分大きい xxx で xL>1≧fn(x)\dfrac{x}{L} > 1 \geqq {f_n} (x)Lx​>1≧fn​(x) です。fn(x)f_n (x)fn​(x) は nnn が増えるにつれ小さい値しか取らなくなるため，十分大きな nnn では，小さい xxx ですでに xL\dfrac{x}{L}Lx​ が fnf_nfn​ の値域を追い越すことになると予想できます。
こうしたイメージを持つと，下図のように nnn を大きく取ると x>πx > \pix>π 以降交点が現れず，答えは 333 になりそうです。
それでは実際に議論していきましょう。
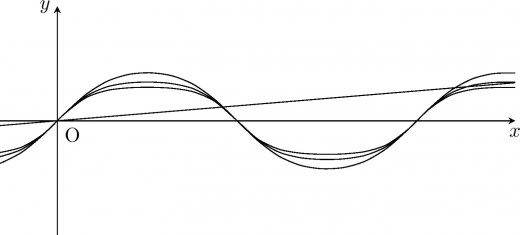
議論証明
前問同様 a=0a=0a=0 は解になる。前問同様 x>0x > 0x>0 の場合を考えれば十分である。また gn(x)=fn(x)−xLg_n (x) = f_n (x) - \dfrac{x}{L}gn​(x)=fn​(x)−Lx​ とおく。
0<x<π0 < x < \pi0<x<π に gn(x)=0g_n (x) = 0gn​(x)=0 の解が存在すること
増減を調べるため fnf_nfn​ の微分を計算する。
fn′(x)=cos⁡(fn−1(x))⋅fn−1′(x)
{f_n}'(x) = \cos (f_{n-1} (x)) \cdot {f_{n-1}}'(x)
fn​′(x)=cos(fn−1​(x))⋅fn−1​′(x)
である。※ f0(x)=xf_0 (x) = xf0​(x)=x として考える。
n≧2n \geqq 2n≧2 の場合，fn−1(x)=sin⁡(fn−2(x))f_{n-1} (x) = \sin (f_{n-2} (x))fn−1​(x)=sin(fn−2​(x)) より
−π2<−1≦fn−1(x)≦1<π2
-\dfrac{\pi}{2} < -1 \leqq f_{n-1} (x) \leqq 1 < \dfrac{\pi}{2}
−2π​<−1≦fn−1​(x)≦1<2π​
より cos⁡(fn−1(x))>0\cos (f_{n-1} (x)) > 0cos(fn−1​(x))>0 である。
前問で示した通り，任意の n≧1n \geqq 1n≧1 に対して fn(0)=0f_n (0) = 0fn​(0)=0 であった。同様に fn(π)=0f_n (\pi) = 0fn​(π)=0 を示すことができるため，特に 
cos⁡(fn(0))=cos⁡(fn(π))=1
\cos (f_n (0)) = \cos (f_n (\pi)) = 1
cos(fn​(0))=cos(fn​(π))=1
である。
以上を用いると帰納的に
x0⋯π2⋯πfn′1+0−−1\begin{array}{c|ccccc}
x & 0 & \cdots & \frac{\pi}{2} & \cdots & \pi\\
\hline
{f_n}' & 1 & + & 0 & - & -1
\end{array}xfn​′​01​⋯+​2π​0​⋯−​π−1​​
と計算される。
次に2階微分を計算する。
fn′′(x)=cos⁡(fn−1(x))⋅fn−1′′(x)−sin⁡(fn−1(x))⋅{fn−1′(x)}2\begin{aligned}
{f_n}'' (x) &= \cos (f_{n-1} (x)) \cdot {f_{n-1}}''(x)\\
&\qquad - \sin (f_{n-1} (x)) \cdot \{ {f_{n-1}}'(x) \}^2 
\end{aligned}fn​′′(x)​=cos(fn−1​(x))⋅fn−1​′′(x)−sin(fn−1​(x))⋅{fn−1​′(x)}2​
0<x<π0 < x < \pi0<x<π で 0<fn−1(x)≦10 < f_{n-1} (x) \leqq 10<fn−1​(x)≦1 であることが帰納的に示されるため，2項目は負である。
これより数学的帰納法によって 0<x<π0 < x < \pi0<x<π で fn′′(x)≦0{f_n}''(x) \leqq 0fn​′′(x)≦0 が従う。
さて，fn′(0)=1{f_n}'(0) = 1fn​′(0)=1，fn′(π)=−1{f_n}' (\pi) = -1fn​′(π)=−1であるため，中間値の定理より 0<cn<π0 < c_n < \pi0<cn​<π であって fn′(c)=1L{f_n}' (c) = \dfrac{1}{L}fn​′(c)=L1​ を満たすものが存在する。0<x<π0 < x < \pi0<x<π で fn′′(x)<0{f_n}''(x) < 0fn​′′(x)<0 より，fn′{f_n}'fn​′ は 000 から π\piπ の間で単調増加であるため，こうした cnc_ncn​ は一意に存在する。
gn(0)=0gn(π)=0−πL<0\begin{aligned}
g_n (0) &= 0\\
g_n (\pi) &= 0 - \dfrac{\pi}{L} < 0
\end{aligned}gn​(0)gn​(π)​=0=0−Lπ​<0​
であり，前の計算から
x0⋯cn⋯πgn′++0−−gn0↗↘−\begin{array}{c|ccccc}
x & 0 & \cdots & c_n & \cdots & \pi\\
\hline
{g_n}' & + & + &0 & - &- \\
{g_n} & 0 & \nearrow & & \searrow & -
\end{array}xgn​′gn​​0+0​⋯+↗​cn​0​⋯−↘​π−−​​
が成り立つ。
よって 0<x<π0 < x < \pi0<x<π の範囲で gn(x)=0g_n (x) = 0gn​(x)=0 を満たす実数が1つ存在する。同様の議論から −π<x<0-\pi < x < 0−π<x<0 の範囲で gn(x)=0g_n (x) = 0gn​(x)=0 を満たす実数が1つ存在する。
こうして AL,n≧3A_{L,n} \geqq 3AL,n​≧3 を得る。
十分大きい nnn で AL,n=3A_{L,n} = 3AL,n​=3 であること
さて，fn(x)f_n (x)fn​(x) は x=π2+2nπ (n∈Z)x = \dfrac{\pi}{2} + 2n \pi \ (n \in \mathbb{Z})x=2π​+2nπ (n∈Z) で極大になる。fnf_nfn​ は周期関数であるため fnf_nfn​ の最大値は fn(π2)f_n \left( \dfrac{\pi}{2} \right)fn​(2π​) となる。
さて，an=fn(π2)a_n = f_n \left( \dfrac{\pi}{2} \right)an​=fn​(2π​) とおく。帰納的に an≠0a_n \neq 0an​=0 が示される。ここで x>0x > 0x>0 で sin⁡x<x\sin x < xsinx<x であるため，
0<an+1=sin⁡an<an
0 < a_{n+1} = \sin a_{n} < a_n
0<an+1​=sinan​<an​
が成り立つ。
問題文中の事実より数列 {an}\{ a_n \}{an​} は収束する。その収束値を α\alphaα とすると sin⁡α=α\sin \alpha = \alphasinα=α が成立する。∣fn(x)∣≦∣sin⁡x∣≦1|f_n (x)| \leqq |\sin x| \leqq 1∣fn​(x)∣≦∣sinx∣≦1 であることから ∣α∣≦1|\alpha| \leqq 1∣α∣≦1 である。この範囲で sin⁡α=α\sin \alpha = \alphasinα=α を満たす実数は α=0\alpha = 0α=0 だけである。
こうして {an}\{ a_n \}{an​} は 000 に収束することが分かった。ゆえに nnn を十分大きくとると an<π2La_n < \dfrac{\pi}{2L}an​<2Lπ​ とできる。
このような nnn について x>πx > \pix>π では
xL>π2L≧fn(x)
\dfrac{x}{L} > \dfrac{\pi}{2L} \geqq f_n (x)
Lx​>2Lπ​≧fn​(x)
である。このとき，AL,n=3A_{L,n} = 3AL,n​=3 である。
こうして
lim⁡n→∞AL,n=3
\lim_{n \to \infty} A_{L,n} = 3
n→∞lim​AL,n​=3
である。

余談

関数 $f_n$ は $n \to \infty$ で $0$ に収束します。

一方 $\begin{aligned} h_1 &= \cos x\\ h_{n+1} &= \cos (h_{n-1} (x)) \end{aligned}$ で定まる関数列は $0$ に収束しません。 $\cos x = x$ の解に収束します。

歴代の大問4の割には解きやすかったかもしれません。とはいえ評価のテクニックが問われる難問であることには間違いありません。