アインシュタイン問題～1つの図形による平面のタイリング

周期的なタイル張りは簡単に構成できます。例えば平行四辺形を使うと次のようなタイル張りができますね。

他にも十字のタイルで平面を敷き詰めることも可能です。

最初の平行四辺形タイルを調整することで次のような敷き詰めも可能です。

このように多角形型のタイリングから曲線によるタイリングが作れます。

上の例は周期的に，つまりタイル全体を並行移動したら元の張り方と一致するようなタイル張りをしています。（平行四辺形1個分/十字1個分ずらしたら全体が重なりますね）

さて，非周期的に（全体を平行移動しても重ならないように）図形を敷き詰めることはできるのでしょうか？

複数の種類の図形を用いたタイル張り

次に示すのはペンローズによる4種類の図形を用いた敷き詰めです。

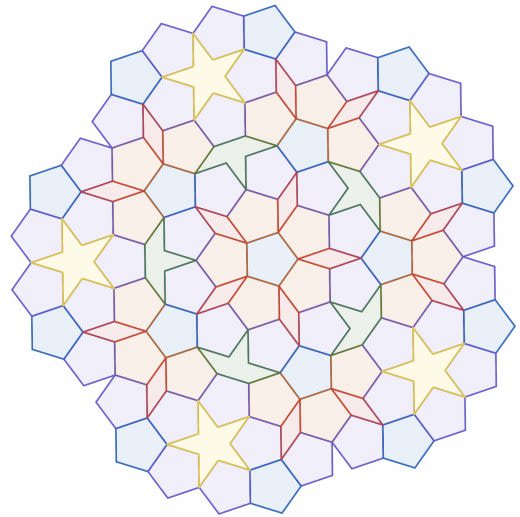
これをペンローズ・タイリングといいます。

中心の五角形から放射状にタイルを繋げていく方法です。「放射状」であるため，このタイル張り全体を並行移動しても元と同じにはなりません。正五角形では平面の敷き詰めが出来ないことに注目して，余る箇所をいい具合に補強したタイリングともいえます。

このタイリングは1970年代に登場し，その後複数回に渡って改善されて2種類のタイルによる非周期的な敷き詰めが発見されています。

1種類の図形を用いたタイル張り

それでは1種類の図形だけでタイリングすることは可能なのでしょうか。この問いは「ein（1つの） stein（石）問題」と名付けられます。

この問いは2023年になってついに解決されました。

裏返しを許すタイリングの例

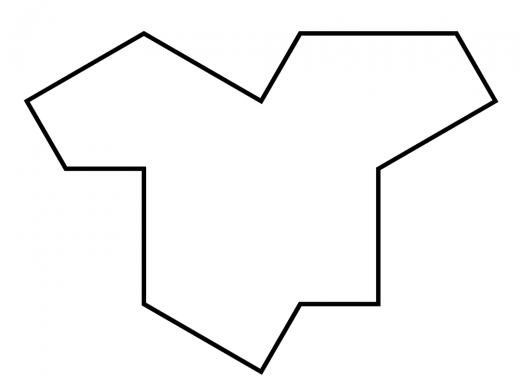
まず．裏返しを許してタイリングが可能である例が発見されます。

これがその図形です。「帽子（hat）」と名付けられています。

帽子は次のように小さいパーツに分割できます。

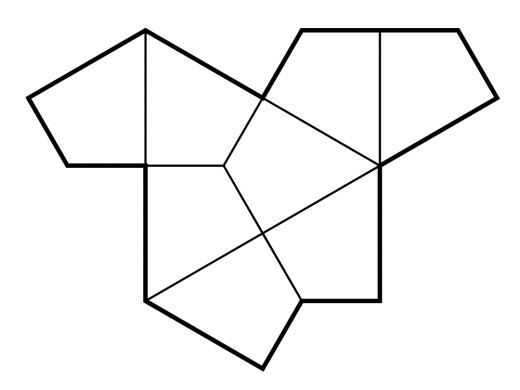
これを基にして次のようなタイリングが可能です。

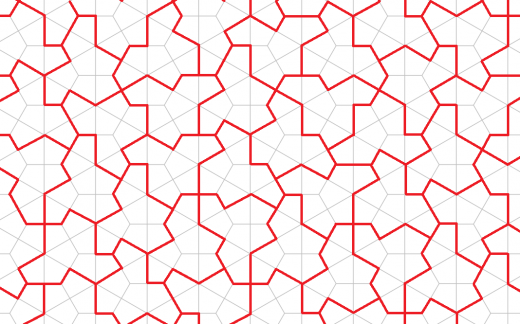
裏返さずにタイリングできる例

裏返してもOKだと，例えタイリングが出来たとしてもちょっと不満が残りますね。

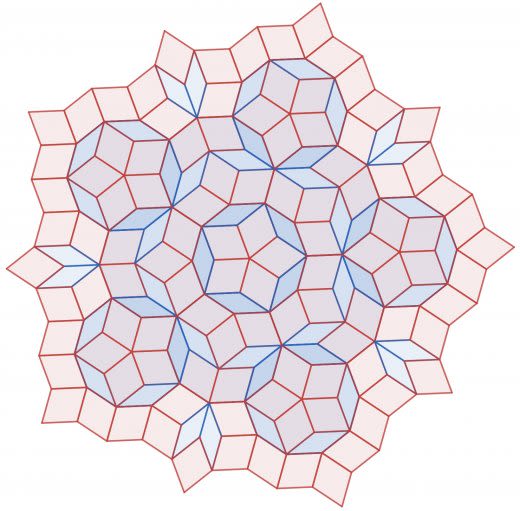
なんと hat を改良することで裏返しせずともタイリングできる図形が発見されます。（ちなみに発見者は hat の発見者と同じです）

これは Spectre と呼ばれます。Spectre によるタイリングを以下に載せます。

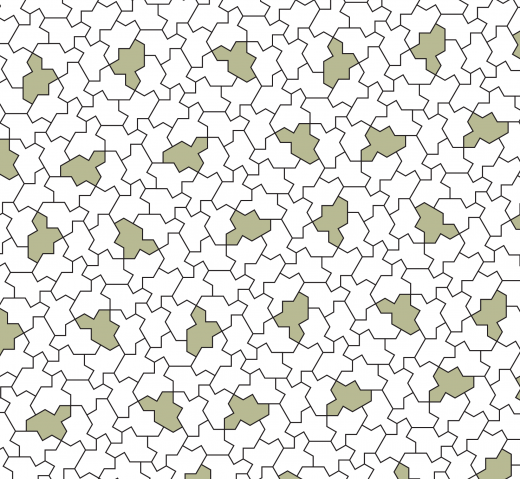
（Smith, David, Joseph Samuel Myers, Craig S. Kaplan and Chaim Goodman-Strauss. “A chiral aperiodic monotile.”（2023）より引用した。）

hat と Spectre が導入された論文はこれらです。arXiv（数学系の論文のプレプリントが掲載されているサイト）から閲覧ができます。

hat の論文

• David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim GoodmanStrauss. An aperiodic monotile, 2023. arXiv:2303.10798.

Spectre の論文

• David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim GoodmanStrauss. A chiral aperiodic monotile, 2023. arXiv:2305.17743.

興味のある人は読んでみてください。