マルコフのディオファントス方程式~東北大AO入試を通して
等式 を満たす正の整数の組は無限個あることを証明せよ。
問題文中の方程式 のことをマルコフのディオファントス方程式といい,その解をマルコフ数といいます。
この記事では,問題の解答を通してマルコフの方程式の解を作るアルゴリズムなどを紹介します。
問題の解答
問題の解答
まず は方程式の正の整数解である。
次に方程式の正の整数解 から新たな解が作られることを示す。
方程式に代入することで は二次方程式 の解である。
判別式は である。
が異なる2解を持つことを示す
が重解を持つと仮定する。このとき つまり, が成立する。これを整理すると となる。
は正の整数であるため, であり, は正の整数である。よって であるが,どの場合も は整数にならない。
こうして矛盾が生じるため, は重解を持たない。
新しい解の構成
前段より は異なる2実数解を持つ。 とは異なる解を とおくと解と係数の関係より つまり, を得る。
は整数であるため も整数であるため, は元の方程式の整数解である。
特に が のうち最小であれば であるため,新たに正の整数解が得られた。さらにこのとき である。実際, より従う。
無限に解を作るアルゴリズム
以上を元に次のステップから新たに解を見つけることができる。
- 正の整数解 を用意する。
- 対称性より を最小の数( に同じ整数があることは認める)として考える。
- が新たな正の整数解として得られる。
前段で述べた通り であるため,必ず元の解と異なるものが得られる。
さらに,このアルゴリズムで解の各成分が減少することはないため,繰り返し操作を行ったとしても元の解に戻ることはない。
こうしてこのアルゴリズムで無数に正の整数解が得られることが示された。
問題を解くポイント
二次方程式の解と係数の関係を使って新しく解を見つけることがポイントです。こうしたテクニックは Vieta jumping とも呼ばれます。詳しくは 数オリのテクニック〜Vieta jumping〜 をご覧ください。
また単にアルゴリズムを提示するだけでは不十分です。落としやすいポイントは:
- アルゴリズムで作った新しい解が正の整数解を与えることの論証を忘れる。
- 新しい解が既存の解と異なることの論証を忘れる。
- 何回か操作を繰り返しても重複がないことの論証を忘れる。
実際に沢山解を作ってみよう
から初めて解を作っていきましょう。
- より を得る。
- より を得る。
- より を得る。
マルコフ数の性質
マルコフ数の性質
不定方程式 をマルコフのディオファントス方程式という。
この方程式は無限に正の整数解を持ち,その解に登場する正の整数をマルコフ数という。
アルゴリズムを通して新たに作られた解と元の解とつなげていくことで二分木を作ることができます。
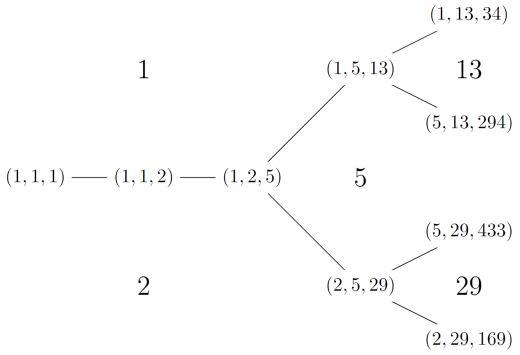
これをマルコフの木といいます。上の図のように解だけではなく,解の成分を「接する」ように書くこともあります。
次の定理は証明は飛ばしますが,非常に重要なものとなります。
マルコフ数は上で紹介したアルゴリズムによってすべて求めることができる。(マルコフの木上にすべての解が存在する)
実はマルコフの木の「実」でマルコフ方程式の解はすべて尽くされるのです。大変興味深い性質です。
原始ピタゴラス数の木 とも似ています。
別解~フィボナッチ数との関連
別解~フィボナッチ数との関連
を 番目のフィボナッチ数とすると が成立する。(数学的帰納法で証明できる)→ フィボナッチ数列の8つの性質(一般項・黄金比・互いに素)
特に を で置き換えると を得る。
ここで に注意すると左辺は と変形される。
よって を得る。
こうして は元の等式の解である。
に対して であるため,無限に解が存在することが分かる。
上の別解をまとめると次のようになります。
奇数番目のフィボナッチ数はマルコフ数である。
パッと見では全く異なる式から出てくる2種類の数に共通点があるのは面白いですね。
類題
類題
以下の問題を類題として紹介します。興味のある方はぜひ解いてみてください。
次の条件を満たす組 を考える。
条件 :,, は正の整数で, および を満たす。
以下の問いに答えよ。
- 条件 を満たす組 で, となるものをすべて求めよ。
- 組 が条件 を満たすとする。このとき,組 が条件 を満たすような が存在することを示せ。
- 条件 を満たす組 は,無数に存在することを示せ。
やはり不定方程式の世界はおもしろいですね。











