デカルトの円定理を2通りの方法で証明します。いずれも考え方は難しくないですが,計算が大変です。各円の中心を O1,O2,O3,O4 とします。
接点三角形に着目した証明
円 Oi と Oj の接点を Tij と書きます。
証明の流れ
- 三角形 T12T13T14 の3辺の長さを r1 から r4 で表す。
- 三角形 T12T13T14 に正弦定理を使って r1 から r4 の間の関係式を導く。

証明1
-
まず,ki=ri1 とおくと,(T12T13)2=(k1+k2)(k1+k3)4 である。これは 接点間の距離に関する有名問題4問 の定理3で紹介しているが,余弦定理を2回使って簡単に導出できる。他の2辺も同様に計算できて,辺の比は
(T12T13)2:(T13T14)2:(T12T14)2=k1+k4:k1+k2:k1+k3
-
三角形 T12T13T14 について,3辺の長さ(の比)がわかったので cos がわかる。よって sin もわかる。一方,三角形の各頂点は O1 上にあるので,外接円の半径は r1 である。よって,正弦定理より
sin∠T12T14T13T12T13=2r1
これで r1 から r4 の間の関係式が得られる。あとは計算するだけ。両辺2乗して変形すると
(T12T13)2=4r12sin2∠T12T14T13
k12(T12T13)2=4(1−cos2∠T12T14T13)
(k1+k2)(k1+k3)4k12=4−4cos2∠T12T14T13
一方,1の結果と余弦定理より,
cos2∠T12T14T13=4(k1+k2)(k1+k3){(k1+k2)+(k1+k3)−(k1+k4)}2=4(k1+k2)(k1+k3)(k1+k2+k3−k4)2
以上より k1 から k4 までの等式を得る:
4k12=4(k1+k2)(k1+k3)−(k1+k2+k3−k4)2
展開すると,
k12+k22+k32+k42=2(k1k2+k1k3+k1k4+k2k3+k2k4+k3k4)
を得る。目標の式は
(k1+k2+k3+k4)2=2(k12+k22+k32+k42)
だが,左辺を展開するとさきほど得た式と一致する。
ヘロンの公式による証明
証明2の概要
三角形 O1O2O3 は,3辺の長さが r1+r2,r2+r3,r3+r1 であるので,ヘロンの公式を使うと面積は,
SO1O2O3=r1r2r3(r1+r2+r3)
 また,大きい三角形を3つの小さい三角形に分割することで,
SO1O2O3=SO1O2O4+SO1O3O4+SO2O3O4
他の三角形の面積も同様に計算できて,両辺を r1r2r3r4 で割って,s=r1+r2+r3+r4 とおくと,
r4s−r4=r3s−r3+r2s−r2+r1s−r1
を得る。頑張って根号を外すなど計算(→補足)すると,デカルトの円定理の式を得る。
また,大きい三角形を3つの小さい三角形に分割することで,
SO1O2O3=SO1O2O4+SO1O3O4+SO2O3O4
他の三角形の面積も同様に計算できて,両辺を r1r2r3r4 で割って,s=r1+r2+r3+r4 とおくと,
r4s−r4=r3s−r3+r2s−r2+r1s−r1
を得る。頑張って根号を外すなど計算(→補足)すると,デカルトの円定理の式を得る。
補足:
根号が4つありますが,移項→両辺2乗 を3回繰り返すと根号を外せます。実際,A−B=C+D
の両辺を2乗すると根号が2つになり,その結果を整理した式
E=F+G
の両辺を2乗すると根号が1つになり,その結果を整理した式
H=I
の両辺を2乗すると根号は消えます。原理は簡単ですが,実際の計算はかなり大変です。
具体的な計算は
A straightforward proof of Descartes’s circle theorem を参照ください。


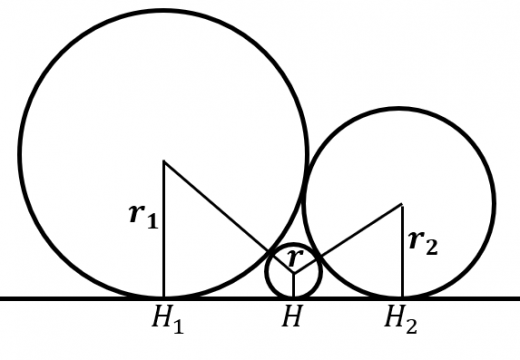 図のように3つの円と1本の直線が互いに接している。3つの円の半径を とするとき,
を示せ。
図のように3つの円と1本の直線が互いに接している。3つの円の半径を とするとき,
を示せ。
 また,大きい三角形を3つの小さい三角形に分割することで,
他の三角形の面積も同様に計算できて,両辺を で割って, とおくと,
を得る。頑張って根号を外すなど計算(→補足)すると,デカルトの円定理の式を得る。
また,大きい三角形を3つの小さい三角形に分割することで,
他の三角形の面積も同様に計算できて,両辺を で割って, とおくと,
を得る。頑張って根号を外すなど計算(→補足)すると,デカルトの円定理の式を得る。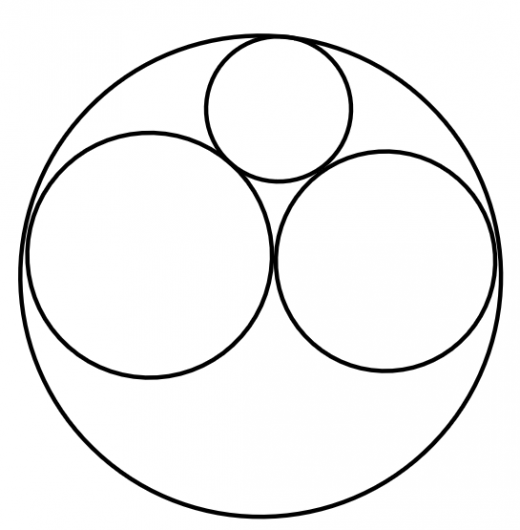 同じく4つの円がそれぞれ互いに接する状況ですが,1つの円が残り3つを含むとき,以下の式が成立します:
同じく4つの円がそれぞれ互いに接する状況ですが,1つの円が残り3つを含むとき,以下の式が成立します:










