接点間の距離に関する有名問題4問(共通接線上の長さなど)
更新
接点間の距離に関する有名な問題を4問まとめました。
問題1と2は基本,3と4は発展です。
共通外接線の接点間の距離
共通外接線の接点間の距離
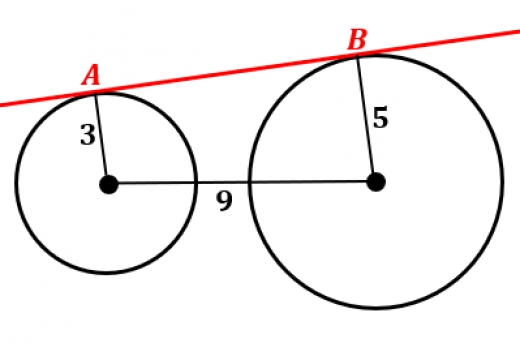 半径が であり,中心間の距離が である2つの円がある。接点間の距離 を求めよ。
半径が であり,中心間の距離が である2つの円がある。接点間の距離 を求めよ。
 図のような直角三角形 に三平方の定理を使うと,
図のような直角三角形 に三平方の定理を使うと,
問題1を一般化すると,以下を得ます。
半径が であり,中心間の距離が である2つの円がある。共通外接線上の2つの接点間の距離 は
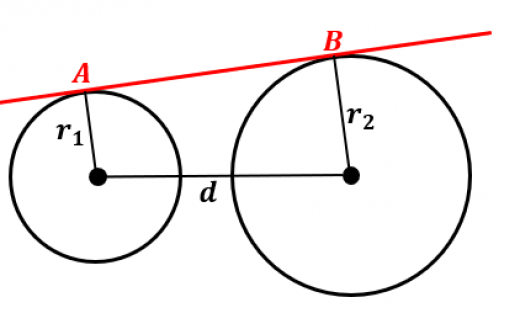
特に,2つの円が接するとき なので,接点間の距離は になります。
共通内接線の接点間の距離
共通内接線の接点間の距離
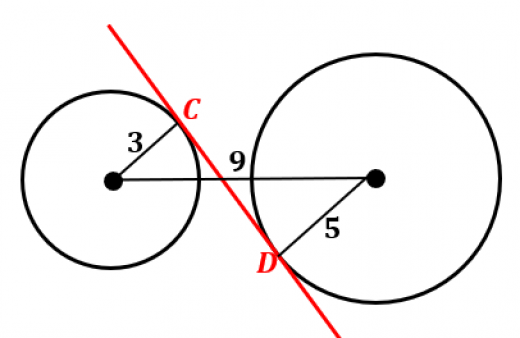 半径が であり,中心間の距離が である2つの円がある。接点間の距離 を求めよ。
半径が であり,中心間の距離が である2つの円がある。接点間の距離 を求めよ。
 図のような直角三角形 に三平方の定理を使うと,
図のような直角三角形 に三平方の定理を使うと,
問題2を一般化すると,以下を得ます。
半径が であり,中心間の距離が である2つの円がある。共通内接線上の2つの接点間の距離 は
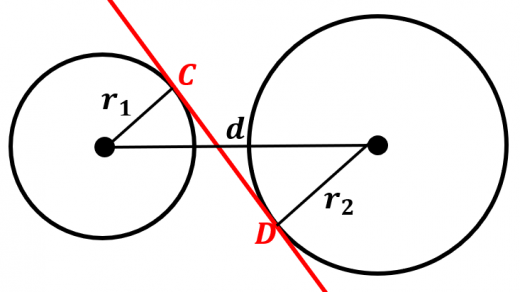
定理1と定理2より,共通外接線の接点間の距離の方が内接線のそれよりも長いことがわかります。
互いに接する3つの円
互いに接する3つの円
半径が である つの円が互いに接している。2つの接点を結ぶ線分 の長さを求めよ。

余弦定理で を求めて,もう一度余弦定理で を求める。
大きい三角形に余弦定理を使うと, さらに,小さい三角形に余弦定理を使うと, よって
問題3を一般化すると,以下を得ます。
半径が である つの円が互いに接している。3つの接点のうち の円周上にある接点を結ぶ線分の長さは
互いに接する3つの円と直線
互いに接する3つの円と直線
問題4の結果はとてもおもしろいです!
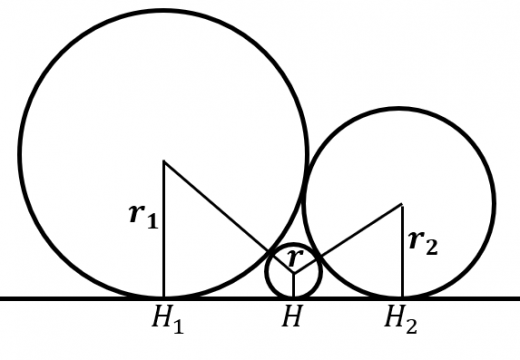 図のように3つの円と1本の直線が互いに接している。3つの円の半径を とするとき,
を示せ。
図のように3つの円と1本の直線が互いに接している。3つの円の半径を とするとき,
を示せ。
直線との接点をそれぞれ とおく。
定理1より,
よって,
両辺を で割ると,
ちなみに,フォードの円では,問題4の構図がたくさん登場します。
「共通接線の長さ」と言ってしまいたいですが,共通接線上の接点間の距離と言うべきですね。











