Sperner の補題と Brouwer の不動点定理
更新
- おもしろい定理を2つ紹介します。Sperner の補題(組合せ論)と Brouwer の不動点定理(解析)です。
- 両方とも証明もおもしろいです。
Sperner の補題
Sperner の補題
まずは,Sperner の補題(スペルナーの補題)です。高校数学の範囲で理解できます。
- 大きい三角形 がある。
- この三角形の周または内部にいくつかの点があり,小さい三角形たちに分割されている。
- 頂点 および各点は赤・青・緑のいずれかで塗られている。ただし以下を満たす:
- は異なる色
- 辺 上の点は または と同じ色
- 辺 上の点は または と同じ色
- 辺 上の点は または と同じ色
このとき, つの頂点の色が相異なるような小さい三角形が存在する。
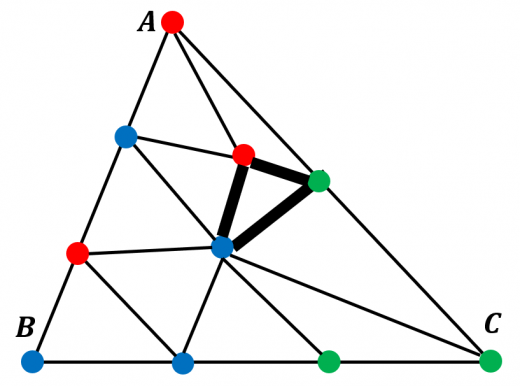
例えば,図において「太線の三角形」は つの頂点の色が異なります。
2次元の場合がおもしろい
2次元の場合がおもしろい
Sperner の補題は 次元単体に関する定理ですが,この記事では2次元の場合のみを紹介します。なぜ2次元かというと「非自明でおもしろい」かつ「イメージしやすい」からです。実際,
- 1次元の場合はほぼ自明な主張です。線分の両端点を異なる2色で塗ったら,途中のどこかで色が(奇数回)切り替わる,というような主張です。
 「中間値の定理の離散バージョン」とも言えます。
「中間値の定理の離散バージョン」とも言えます。
※なお,1次元の場合の Sperner の補題の証明(とほぼ同じ意味の問題)が東大文系数学2002年第4問で出題されています。 - 3次元以上だとイメージしにくいです。例えば3次元の場合,大きい四面体を小さい四面体に分割して各頂点を4色のいずれかで塗る状況になります。
Sperner の補題の証明
Sperner の補題の証明
それでは2次元の場合の Sperner の補題を証明します。
点 が赤色,点 が青色の状況を考えても一般性を失わない。
図のように「赤と青の辺」に矢印を引く。

仮定より辺 をまたぐ矢印は無く,(1次元の場合の Sperner の補題より)辺 をまたぐ矢印が奇数本存在する。
そこで,その奇数本の中から1本選んで矢印をたどっていく(各小さい三角形から伸びる矢印は 本以下なので途中で分岐することはない)。
すると,以下のいずれかになる。
- 状況1. 外側に戻ってくる
- 状況2. 内部で行き止まりに到達する
状況2が必ずどこかで発生する。なぜなら をまたぐ矢印が奇数本存在するためである。
そして状況2の行き止まりは, つの頂点の色が相異なるような小さい三角形になる。
Brouwer の不動点定理
Brouwer の不動点定理
Sperner の補題の重要な応用例として「Brouwer(ブラウワー)の不動点定理の証明」があります。
次元球 から への連続関数 には必ず不動点が存在する。つまり,ある が存在して
次元球 とはユークリッド空間 においてある点からの距離が一定値以下である点の集合です。
例えば の場合,「定義域が であり も におさまるような連続関数 に対して, を満たす が存在する」という定理です。
※より一般に, を「ユークリッド空間 のコンパクト凸集合」としても定理は成立します。
Brouwer の不動点定理の証明
Spernerの補題(2次元の場合)を使って Brouwer の不動点定理(2次元の場合)を証明します。一般の 次元の場合も同様です。
とする。正三角形 (の周と内部全体)を と書く。
目標は「 から への連続関数に対する不動点の存在」を示すことだが,以下では「 から への連続関数に対する不動点の存在」を示す。
( と は「だいたい同じ」なので で示せば十分。厳密には, と は位相同型(連続な全単射で逆写像も連続なものが存在)であることからOK)
を細かく三角形分割していく(例えば中点三角形で分割など,すべての小さい三角形の各辺の長さが に限りなく近づくように)。 段階目の三角形分割を とおく。 は の細分である。

の各点 に以下のように色を塗る:
- の第1成分が より第1成分が小さいなら赤
- の第2成分が より第2成分が小さいなら青
- の第3成分が より第3成分が小さいなら緑
で塗る(複数該当ならどれでもよい)。 上の点は3つの成分の和が で一定なので上記1~3をいずれも満たさないなら と の各成分は等しいので が不動点。もし不動点が存在しないならこのような三角形分割をひたすら続ける。
上記の塗り方により,三角形分割 は Spernerの補題の前提を満たすので3つの頂点の色が相異なるような小さい三角形 が存在する。このとき, は赤, は青, は緑で塗られているとする。
点列 を考える。 はコンパクト(有界閉)なので収束部分列 を持つ。この収束先を とおく。
このとき「各 は赤で塗られている」ことと「 は連続」より
- の第1成分は の第1成分以下
一方,三角形分割で各三角形のサイズは に近づくので でもある。よって,
- の第2成分は の第2成分以下
第3成分も同様である。ところが, と の各成分の和は で等しいので結局各成分が等しい。つまり が不動点。
参考文献:MAT307-lecture03.pdf
Brouwer の不動点定理の証明は,細部まで理解するのがけっこう大変ですが,細分まで理解する価値があります。











