逆正弦法則の意味と導出
ランダムウォークにおける逆正弦法則について紹介します。大雑把に言うと,ほとんどの人は「ずっと勝っている状態」または「ずっと負けている状態」になるという話です。
途中の「おもしろい補題」は高校数学でも理解できます。
問題設定
問題設定
-
一次元のランダムウォークを考えます。
-
つまり,確率 で ポイント,確率 で ポイントとなるゲームを繰り返す状況を考えます。
-
例えば,コイントスを行い,勝ったら1円もらえ負けたら1円失うようなゲームを繰り返すイメージです。
-
例として, となった状況を図に示します。8回繰り返して最終 ポイントです。

逆正弦法則
逆正弦法則
「逆正弦法則」と呼ばれる法則を2種類紹介します。
1. プラスの状態にいた時間の割合
「プラスの状態にいた時間の割合 」が従う分布を考えます。例えば, と遷移した場合,プラスの状態にいた時間の割合は図の赤い部分で です。
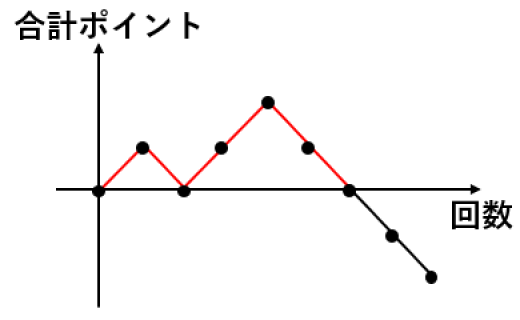
試行回数が十分大きいとき,「プラスの状態にいた時間の割合 」が従う分布は,逆正弦分布に近づく。
ただし,この記事では以下の分布を逆正弦分布と呼ぶ。
A. 確率密度関数は
B. 累積分布関数は
- 確率密度関数のグラフを描いてみます。当たり前ですが に関して対称です。 でへこんでいて, 付近が高いです。つまり,多くの場合「ずっとプラス」または「ずっとマイナス」というわけです。

- 累積分布関数には逆三角関数が登場します。→逆三角関数(Arcsin,Arccos,Arctan)の意味と性質
「逆正弦法則」と呼ばれる由来です。 - AとBの関係を確認しておきます。
を微分して になることを確認する。
および合成関数の微分公式より
また, であることもわかる。
2.最後に0に戻ってきてからの時間の割合
2つめの逆正弦法則です。「プラスの状態にいた時間の割合 」が従う分布を考えます。例えば, と遷移した場合,最後に0に戻ってきてからの時間の割合は です。

試行回数が十分大きいとき,「最後に0に戻ってきてから現在までの時間の割合 」が従う分布は,逆正弦分布に近づく。
おもしろい補題
おもしろい補題
逆正弦法則の導出に向けて,おもしろい補題を紹介します。以下の補題は,
- 逆正弦法則1と2の導出で使います。
- 以下の補題だけなら高校数学範囲内で証明できます。
試行回数 のとき,以下はすべて と等しい。
(a) 回終了時に にいる確率
(b) 回目まで に1回も戻らない確率
© 回目までずっと 以上である確率
-
(a) は簡単。 回のうち 回 で 回 になる場合の数は
-
©=(a) を示す。一番大変。
「 回終了時に にいる (a) のパターン」と「 回目までずっと 以上である © のパターン」の間に1対1対応があることを示せばよい。 (a) のパターンに対して,
「最初に最小値を達成した点 までの部分を切って 軸に関して折り返して末尾につけて原点を に平行移動する」
と © のパターンになる。 逆の操作も構成できる。つまり,©のパターンに対して
逆の操作も構成できる。つまり,©のパターンに対して
「はじめて最終累積値の半分まで戻った点 まで切って折り返して最初につけて原点を先頭の点に平行移動する」ともとの(a)のパターンに戻る。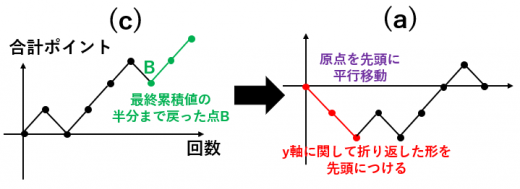
-
(b)=© を示す。文章は長いが難しくない。
- 「 回目まで0に1回も戻らない (b) のパターン」のうち「最初に+1」となるのは半分である。
- 「 回目までずっと 以上である © のパターン」のうち「最後に+1」となるのは半分である。なぜなら, 回目終了時は奇数ポイントなので,その時点までで © のパターンか否かが決まるからである。
- 以上から「(b) のパターンのうち最初に+1のもの」と「© のパターンのうち最後に+1のもの」の間に1対1対応があることを示せばよい。
「(b) のパターンのうち最初に+1のもの」に対して「最初の1回分を無視して,最後の1回に をつける」と © のパターンになる。逆に「© のパターンのうち最後に+1のもの」に対して「最後の1回分を無視して,最初の1回に をつける」と元に戻る。
逆正弦法則2の導出
逆正弦法則2の導出
さきほどの補題とスターリングの公式を使えば逆正弦法則2は簡単に導出できます。
まず,試行回数が のとき, であることを示す。
となるのは, 回のうち「最初の 回終了時に0にいる」かつ「後半の 回で0に1回も戻らない」なので,補題の(a)と(b)より定理が成立。
次に, を評価する。
スターリングの公式 より,
以上より,
つまり が十分大きいとき, は確率密度関数が である分布に近づく(区分求積法)。
参考文献
逆正弦法則1の証明は,2の証明と似ています。同じように であることを示します。その後は全く同じです。ただし,紫色の式を示すために上記の補題に加えて数学的帰納法を使い,もう少し頑張る必要があります。→逆正弦法則の「できるだけ直感的な」証明
「おもしろい補題→スターリングの公式→積分してArcsinが出てくる」という一連の流れがとても楽しいです。











