2曲線が接する3通りの条件
更新
「接する2つの曲線」に関する問題について,3通りの解き方を紹介します。
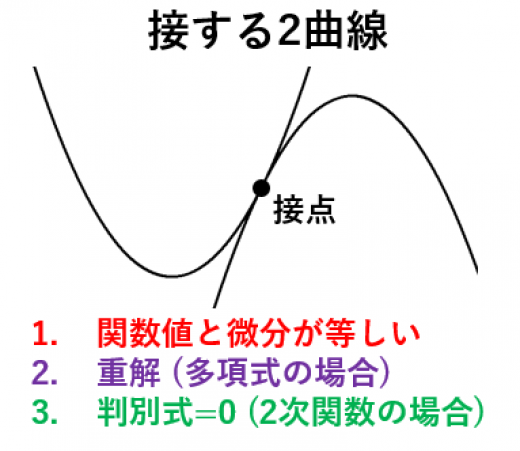
2曲線が接するとは
2曲線が接するとは
と が で接する
かつ
つまり,2曲線が接するとは,その点において関数の値と微分係数が等しいことを表します。
と が接するとき, の値を求めよ。また,接点における接線の方程式を求めよ。

で2曲線が接するとき,
- より
- より
よって,2つめの式から
さらに1つめの式に代入して
より
また, より, の における接線の方程式は,
重解による条件
重解による条件
2曲線がいずれも多項式で表せる場合,接する条件は重解を持つと言い換えることができます。
と が多項式のとき,
と が で接する
かつ
は を重解に持つ
赤の条件と紫の条件が同値であることは,因数定理からわかります。→因数定理の意味と因数分解への応用・重解バージョンの証明
重解の条件を使うとさきほどの例題が少し楽に解けます。
が重解を持つので,実数 を用いて
とおける。2乗の係数を比較して となる。両辺整理すると
係数比較して
接線の方程式はさきほどと同様に求まる。
判別式による条件
判別式による条件
さらに,二次関数の場合は重解を持つは判別式=0と言い換えできます。
の判別式が なので,
つまり
※結局接点の座標 を求めるために別途計算しないといけないです。 を求めるだけならこの解法が早いです。
「曲線が接する」の補足
「曲線が接する」の補足
-
その点での値と微分係数が同じとき,2つの曲線は接すると言うのでした。
-
接する2つの曲線において,特に片方が直線のとき,もう片方の接線と言います。
-
例えば, に対して は接線です。貫通しているので「接しているのか?」という気持ちになりますが「その点での値と微分係数は同じ」なので接すると言えます。

練習問題
練習問題
と が接するとき の値を求めよ。
多項式なので重解の条件を使ってみる。
で接するとき,
とおける( で重解かつ は明らかに共有点なので)。
展開して係数を比較すると,
これを解くと
よって
かつ という条件を使って解いてみる。
- のとき,
- のとき1つめの式より
は不適より
これを2つめの式に代入すると
このとき
と が接するとき の値を求めよ。
数学IIIの範囲です。対数関数 が登場しています。
多項式でないので, かつ という条件を使う。
で接するとき,
- より
- より
2つめの式より ,対数関数の定義域から より
これを1つめの式に代入すると
大学入試では「曲線と直線が接する問題」が多いですが「両方とも直線でない曲線」が接する問題もおもしろいです。











