確率漸化式の解き方と例題

求める確率を $a_n$ とおく。

$n$ 回目の合計が奇数になるのは以下の2パターン。

• $n-1$ 回目までの合計が奇数で，$n$ 回目が偶数
  このようになる確率は $a_{n-1}\times\dfrac{2}{5}$
• $n-1$ 回目までの合計が偶数で，$n$ 回目が奇数
  このようになる確率は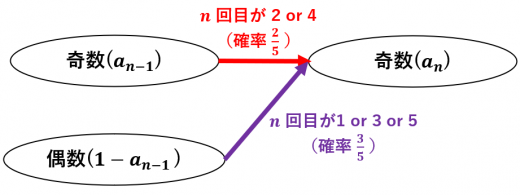 $(1-a_{n-1})\times\dfrac{3}{5}$

よって，

$$\begin{aligned} a_n &= \dfrac{2}{5}a_{n-1}+\dfrac{3}{5} (1-a_{n-1})\\ &= -\dfrac{1}{5}a_{n-1}+\dfrac{3}{5} \end{aligned}$$

この漸化式の特性方程式は $\alpha=-\dfrac{1}{5}\alpha+\dfrac{3}{5}$ であり解は $\alpha=\dfrac{1}{2}$

よって，

$$a_n-\dfrac{1}{2}=\left(-\dfrac{1}{5}\right)^{n-1}\left(a_1-\dfrac{1}{2}\right)$$

$a_1=\dfrac{3}{5}$ より，求めるものは $$a_n=\dfrac{1}{2}+\dfrac{1}{10}\left(-\dfrac{1}{5}\right)^{n-1}$$ となる。

まず，何回目かの操作の後にちょうど $n$ 段目にいる確率を $p_n$ とおく。

$n$ が $3$ 以上の場合について，以下のように状態を遷移図に表す。

遷移図を元に考えると， $$p_n = \dfrac{1}{2}p_{n-1} +\dfrac{1}{2}p_{n-2}\quad(n \geqq 3)$$

漸化式は以下のように変形できる： $$\begin{aligned} p_n - p_{n-1} &= -\dfrac{1}{2}\left(p_{n-1}-p_{n-2}\right) &(n \geqq 3)\\ p_n + \dfrac{1}{2}p_{n-1} &= p_{n-1} +\dfrac{1}{2} p_{n-2} &(n \geqq 3) \end{aligned}$$

$p_1 = \dfrac{1}{2},\:p_2 = \dfrac{3}{4}$ に注意すると，二つの漸化式のそれぞれの一般項は

$$\begin{aligned} p_{n+1} - p_n &= (p_2 -p_1)\left(-\dfrac{1}{2}\right)^{n-1}\\ &=\left(-\dfrac{1}{2}\right)^{n+1} &(n \geqq 3)\\ p_{n+1} + \dfrac{1}{2}p_n&=p_2 +\dfrac{1}{2}p_1 \\ &= 1 &(n \geqq 3) \end{aligned}$$

両辺を引くと， $$\dfrac{3}{2}p_n=1 -\left(-\dfrac{1}{2}\right)^{n+1}\quad(n \leqq 3)$$ $p_n$ について解くと， $$p_n=\dfrac{2}{3}+\dfrac{1}{3}\left(-\dfrac{1}{2}\right)^n \quad(n \geqq 3)$$

$n=1,n=2$ のときもこれを満たすので， $$p_n = \dfrac{2}{3}+\dfrac{1}{3}\left(-\dfrac{1}{2}\right)^n$$

$n$ 回目に $3$ の倍数である確率は $b_n$ と設定されている。

また，$3$ で割った余りが $1$ である場合と $2$ である場合は対称性より，どちらも確率を $c_n$ とおける。

このとき，以下の遷移図が書ける。

確率の総和は $1$ なので，$2c_n+b_n = 1$ となる。つまり，

$$c_n = \dfrac{1}{2}(1 - b_n)$$

また，遷移図を元に考えると，

$$b_{n+1} = \dfrac{1}{3}b_n +\dfrac{2}{3}c_n \quad(n \geqq 1)$$

となる。この2つから $c_n$ を消去すると，

$$b_{n+1} = \dfrac{1}{3}\quad(n \geqq 1)$$

つまり，$b_n = \dfrac{1}{3} \quad(n \geqq 2)$

$b_1 = \dfrac{1}{3}$ と合わせて，$b_n = \dfrac{1}{3}$