必要条件と十分条件の意味・3つの覚え方・例題
必要条件・十分条件・必要十分条件 について,基礎からわかりやすく解説します。
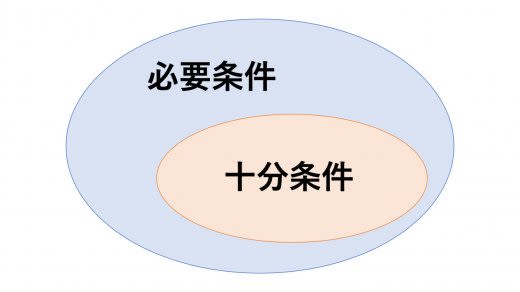
必要条件,十分条件とは
必要条件,十分条件とは
「 ならば が成立する」が真であるとき,
- はの 必要条件 である,と言います。
- はの 十分条件 である,と言います。
東京に住んでいるならば確実に日本に住んでいると言えます。つまり,
- 「日本に住んでいる」は「東京に住んでいる」の 必要条件 です。
- 「東京に住んでいる」は「日本に住んでいる」の 十分条件 です。
「」ならば 「 は偶数」です。つまり,
- 「 は偶数」は「」の 必要条件 です。
- 「」は「 は偶数」の 十分条件 です。
必要条件・十分条件は,数学のどの分野でも登場する,非常に重要な考え方です。
※様々な論証の方法については 集合,命題,論証 にまとめてあります。
必要条件と十分条件の覚え方
必要条件と十分条件の覚え方
「 ならば 」のとき,どちらが必要条件で,どちらが十分条件だっけ…? と困らないように,必要条件と十分条件の覚え方を3つ紹介します。一番しっくりくる方法で覚えてください。
覚え方1. 「必要」と「十分」の意味で覚える
-
「 ならば 」
→「 が成り立つには が必要」
→ が必要条件 -
「 ならば 」
→「 が成り立つためには が成り立てば十分」
→ が十分条件
「東京に住んでいる」ならば「日本に住んでいる」だが,
- 「東京に住んでいる」には
「日本に住んでいる」が必要
→ 「日本に住んでいる」が必要条件 - 「日本に住んでいる」ためには「東京に住んでいる」なら十分
→ 「東京に住んでいる」が十分条件
覚え方2.「矢印の先が必要条件」
「 ならば 」を矢印を使って「」と書いたとき,矢印の先が必要条件と覚えます。
左から順に「じゅうよう」と語呂で覚えても良いでしょう。

覚え方3.「包含関係でイメージ:大きいほうが必要条件」
「 ならば 」をベン図(包含関係)で表すと, が に含まれる図になります。図で大きい方が必要条件と覚えます。

集合については以下の記事もおすすめです。
必要十分条件とは
必要十分条件とは
必要条件でもあり,十分条件でもあるとき,必要十分条件と言います。
つまり,「 ならば 」と「 ならば 」が両方成立するとき,
- 「 は の必要十分条件」と言います。
- 「 は の必要十分条件」とも言います。
- 「 と は同値である」とも言います。
例えばサイコロを1個ふって出た目を とするとき「 が偶数」は「 が のいずれか」の必要十分条件です。
必要条件と十分条件を判定する例題
必要条件と十分条件を判定する例題
必要条件・十分条件に関する例題を解いてみます。以下のそれぞれについて, は のどのような条件になっているでしょうか?
- は奇数

- ならば は奇数である
- が奇数だからといって, とは限らない。(反例:)
よって, は の十分条件だが,必要条件ではない。
- または ,
- または
なので,
- 「 ならば 」は成立しない(反例:)
- 「 ならば 」も成立しない(反例:)
よって, は の必要条件でも十分条件でもない。
三角形 の各辺 上に点 があるもとで,
- が一点で交わる
- 「 ならば 」は成立(チェバの定理)
- 「 ならば 」も成立(チェバの定理の逆)
よって, は の必要十分条件である。
- :関数 が で連続
- :関数 が で微分可能
詳細は関数の連続性と微分可能性の意味と関係で解説しています。
- 「 ならば 」は成立しない(反例:)
- 「 ならば 」は成立する(有名で重要な事実)
よって, は の必要条件だが,十分条件ではない。
必要条件と十分条件を判定する方法
必要条件と十分条件を判定する方法
上記では「 が の必要条件か十分条件かを判定する問題」を解きました。このような問題では,
- 「 ならば 」
- 「 ならば 」
がそれぞれ成立するのかしないのかを判定する必要があります。 そして,「 ならば 」が成立するか判定するには,以下のいずれかをやる必要があります。
- 「 ならば 」が成立することを証明(簡単な説明)する
- なのに でない例(反例)を挙げる
必要条件と十分条件の見分け方
必要条件と十分条件の見分け方
必要条件と十分条件について,下図のような見分け方の表を作ることができます。問題を解く際の参考にしてください。

英語
英語
-
必要条件は英語で necessary condition と言います。
-
十分条件は英語で sufficient condition と言います。
-
必要十分条件は,necessary and sufficient condition と言うこともありますが,以下のようにいろいろな表現があります。
- if and only if
「もし ならば,そしてそのときに限り 」という意味です。 - iff
- if and only if
「当サイトを知っている」ことが「数学が得意である」の必要条件になると嬉しいです!











