漸化式を用いた関数方程式の解法

更新 2021/03/07

$x,f(x),f(f(x)),f(f(f(x)))\cdots$ のみの関数方程式は漸化式を用いると解けることがある

このテクニックを用いる問題の出題頻度は高くありませんが，もし出題された場合に漸化式による解法を知らないと厳しいので一応知っておいた方がよいと思います。

関数を繰り返し適用することで得られる数列を考える

適当な初期値
a0a_0a0​
 と関数
f(x)f(x)f(x)
 を持ってくれば
a0a_0a0​
 に関数を繰り返し適用することで数列が得られます。
（ただし，このような数列を考えるためには関数の定義域が値域を含んでいる必要があります。）
つまり，漸化式
an+1=f(an)a_{n+1}=f(a_n)an+1​=f(an​)
 によって数列を生み出すのです。
例
関数
f(x)=x2f(x)=x^2f(x)=x2
 と初期値
a0=2a_0=2a0​=2
 に対して，a1=4,a2=16,a3=256⋯a_1=4,a_2=16,a_3=256\cdotsa1​=4,a2​=16,a3​=256⋯
 という数列が得られる
ちなみに，この
「関数＋初期値→数列」という構図は入試問題（不動点定理を背景とした極限の問題など）でもわりと出題されるので関数を繰り返し適用することで数列が生成されるというのは意識しておきましょう。
次に，この考え方が関数方程式に応用できることを説明します。

関数方程式への応用

「関数に対応する数列」が定義されることが分かりました。（関数→数列はいつもOK）
逆に，関数がわからなくても「関数に対応する数列」が分かればもとの関数を再現できる場合があります。（数列→関数はしばしばOK）
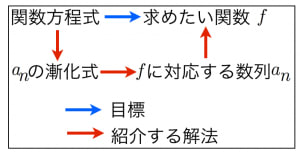
そこで，
関数方程式から「関数」が求まらなくても「関数に対応するする数列」を求めることができればよいわけです。
そして，x,f(x),f(f(x)),f(f(f(x)))⋯x,f(x),f(f(x)),f(f(f(x)))\cdotsx,f(x),f(f(x)),f(f(f(x)))⋯
 のみの関数方程式は「関数に対応する数列」の漸化式を表しているので，その漸化式を解けば関数を復元できるのです！
例
関数方程式
f(f(x))+f(x)=2x+3f(f(x))+f(x)=2x+3f(f(x))+f(x)=2x+3
 は，
（an+1=f(an)a_{n+1}=f(a_n)an+1​=f(an​)
 で定義される数列に対して）
漸化式
an+2+an+1=2an+3a_{n+2}+a_{n+1}=2a_n+3an+2​+an+1​=2an​+3
 が成立することを表しているので，これを解けば何かよいことがあるかもしれない
実際は「関数に対応する数列」の一般項から関数を復元する部分で一工夫必要になりますが，基本的な考え方はこんな感じです。
それでは，実際に漸化式を用いて関数方程式を解く例を見てみましょう。

数学オリンピックの問題

IMO 1992 Shortlist（数学オリンピックの問題の候補になったもの）の問題を紹介します。

問題

$f(f(x))+af(x)=b(a+b)x$ を満たす関数 $f$ を求めよ。ただし， $a,b$ は正の実数で， $f$ は正の実数全体から正の実数全体への関数とする。

方針

漸化式をたてて解くところまでは機械的にできます。（→三項間漸化式の3通りの解き方）値域が正の実数全体という性質を利用して漸化式から数列を復元します。

解答

関数方程式に対応する漸化式は $a_{n+2}+aa_{n+1}=b(a+b)a_n$

これは三項間漸化式なので一般項を求めると，

$a_{n}=Ab^n+B(-a-b)^n$

ただし， $A,B$ は初期条件によって決まる定数。

また，全ての自然数 $n$ に対して $a_n > 0$ となるためには $B=0$ が必要（そうでないと十分大きい $n$ に対して $a_n$ は振動する）。

また， $n=0$ として $A=a_0$ が分かる。

よって， $a_{n}=a_0b^n$ となり， $a_1=ba_0$

これが任意の初期値 $a_0$ に対して成り立つので， $f(x)=bx$ が必要条件。そして，実際に $f(x)=bx$ は関数方程式を満たす。

注：定数の $a$ と数列の $a_n$ が混在して少し見にくくなりました，すみません。

漸化式は関数方程式の一種です。

Tag:漸化式の解き方11パターンと応用例まとめ

Tag:各地の数オリの過去問

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！