Weitzenböckの不等式

ヘロンの公式より，

$$S^2=\dfrac{1}{16} (a+b+c)(a+b-c)(a-b+c)(-a+b+c)$$ なので，証明すべき不等式は以下と同値である。

$$(a^2+b^2+c^2)^2 \geq 48 \cdot \dfrac{1}{16} (a+b+c)(a+b-c)(a-b+c)(-a+b+c)$$

両辺を展開して整理すると，証明すべき不等式はいかのように同値変形していける。

$$\begin{aligned} &a^4+b^4+c^4+2(a^2b^2+b^2c^2+c^2a^2)\\ &\geq -3(a^4+b^4+c^4)+6(a^2b^2+b^2c^2+c^2a^2)\\ &a^4+b^4+c^4-(a^2b^2+b^2c^2+c^2a^2)\geq 0\\ &\dfrac{1}{2}\{(a^2-b^2)^2+(b^2-c^2)^2+(c^2-a^2)^2\}\geq 0 \end{aligned}$$

この最後の不等式は明らかに成立する。

よって，Weitzenböckの不等式が示された。

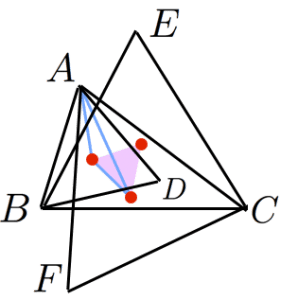
（三角形 $ABC$ の内側の向きに）三角形 $ABD, BCE, CAF$ が正三角形となるように点 $D, E, F$ を取る。また，3つの正三角形の重心を $P, Q, R$ とおく（図の赤い点）。

重心は中線を $2:1$ に内分するので，$AP=\dfrac{\sqrt{3}}{2}c\times \dfrac{2}{3}=\dfrac{c}{\sqrt{3}}$

同様に，$AR=\dfrac{b}{\sqrt{3}}$

また，$\angle PAR=|A-60^{\circ}|$

よって，三角形 $APR$ （青い三角形）に余弦定理を用いて $PR$ が求まる：

$$\begin{aligned} PR^2 &= \dfrac{b^2}{3}+\dfrac{c^2}{3}-\dfrac{2bc}{3}\cos (A-60^{\circ})\\ &=\dfrac{1}{3} (b^2+c^2-bc\cos A-\sqrt{3}bc\sin A)\\ &=\dfrac{1}{3}\left\{b^2+c^2-\dfrac{b^2+c^2-a^2}{2}-2\sqrt{3}\times \dfrac{1}{2}bc\sin A\right\}\\ &=\dfrac{1}{6} (a^2+b^2+c^2-4\sqrt{3}S) \end{aligned}$$

$PR^2\geq 0$ なのでWeitzenböckの不等式が証明された。

余弦定理より，$c^2=a^2+b^2-2ab\cos C$

三角形の面積公式より $S=\dfrac{1}{2}ab\sin C$

以上より，目標の不等式の両辺の差は，

$$\begin{aligned} &a^2+b^2+c^2-4\sqrt{3}S\\ &=2a^2+2b^2-2ab\cos C-2\sqrt{3}ab\sin C\\ &=2(a^2+b^2-ab\cos C-ab\sqrt{3}\sin C) \end{aligned}$$

となる。さらに三角関数の合成公式を使うと，上式$\times\dfrac{1}{2}$ は

$$\begin{aligned} &a^2+b^2-2ab\sin \left(C+30^{\circ}\right)\\ &=(a-b)^2+2ab\left\{1-\sin\left(C+30^{\circ}\right)\right\} \geq 0 \end{aligned}$$

となる。等号成立条件は $a=b$ かつ $C=60^{\circ}$，つまり正三角形。