位相空間論の基礎~連結空間・弧状連結空間の意味
更新
-
位相空間 が連結空間であるとは,次の条件を満たす開部分集合 が存在しないことをいう。
-
位相空間 が弧状連結空間であるとは,任意の に対して,連続写像 であって, となるものが取れることをいう。この連続写像を道という。
この記事では連結空間について解説します。
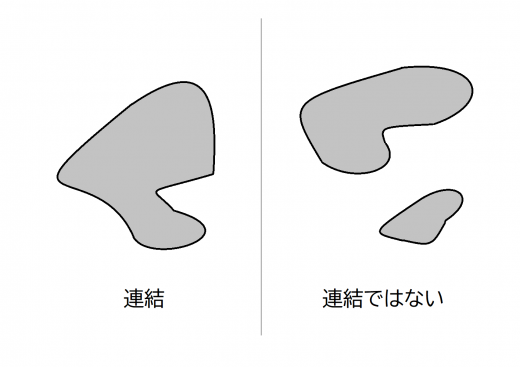
連結性は位相空間が「つながっているのか」を示す指標です。様々な分野で登場するためしっかりと理解しましょう。
例~実数の連結・弧状連結性
例~実数の連結・弧状連結性
実数直線 は連結であり,弧状連結である。
弧状連結性
弧状連結であることの証明は簡単です。
を任意に取る。 と定めればよい。
連結性
連結であることの証明は少々長いです。
基本的に連結であることを示す方法は2ステップに分かれます。
- 連結ではないと仮定して,条件を満たす開集合 を取る。
- 頑張って矛盾を導く。
今回の場合,次の命題を用います。
を の開集合とする。
に対して,ある正の実数 が存在し となる。
この命題は開集合が内点からなること・内点の定義から従います。→ 距離空間~位相空間論に向けた開集合・閉集合の一般化
連結ではないと仮定する。このとき,, となる空ではない開部分集合 が存在する。
を固定する。このとき を と定める。
- がどちらも存在しない場合
がどちらも存在しない場合( の場合), となるため, である。これは と矛盾する。
- が存在する場合
とおく。
と仮定する。 は開集合であったため, となるように正の実数 を取ることができる。しかしこのとき となり, が下限であることに反する。
であるとき, から となる。 は開集合であるため, となるような正の実数 が存在する。一方, であったため, となる。これより となり矛盾する。
- が存在する場合
についても同様に矛盾が示される。
こうして は連結になる。
このように
- から が矛盾することを示す
- から が矛盾することを示す
のいずれかを示すことを意識するといいでしょう。
連結空間の性質
連結空間の性質
連結性の特徴付け
連結性の特徴付けを紹介します。
まず連結空間には開かつ閉な部分集合がさっぱり存在しません。
また連結空間から2点集合への連続写像には非常に重要な性質があります。
位相空間 について次の3つは同値となる。
- は連結である。
- が開かつ閉である場合, か となる。
- 2点集合への連続写像 は常に定数写像である。ただし, には離散位相の構造(すべての部分集合が開)を入れている。
を開かつ閉な部分集合とする。
である。また, は閉であるため は開集合になる。定義より である。
がどちらも空でないことは の連結性と矛盾するため, のいずれかは である。よって は か のいずれかである。
2点集合への写像がつねに一定の値を取ることを示せばよいため, が全射でないことを示せば十分である。
が全射と仮定すると は開かつ閉になる。( は離散位相が入るため は開かつ閉であるため)
2の過程より は もしくは となるが,どちらも の全射性と矛盾する。
対偶を示す。
連結でない場合,, となる開集合 を取ることができる。 を と定めると 3 の条件を満たさない連続写像を得る。
例を見てみましょう。
離散集合への連続関数 は,常に定数関数になる。
よって,3が成立するため は連結である。
同様の議論により も連結であることが簡単に分かる。
2点集合への連続写像の活用
前述の定理で登場した「連結であることと2点集合への連続写像が定数であることの同値性」を用いて様々な性質を示します。
連結空間の像
を連結空間, を位相空間として を連続写像とする。
このとき は連結空間である。
を連続写像とする。
このとき,連続写像 が得られる。
の連結性より は定数写像である。 の取る値を とおく。
を任意に取ると,ある があって である。ゆえに となり, が定数写像であることが分かる。
連結空間の積
を連結空間とする。このとき は連結空間である。
を連続関数とする。これが定数写像であることを示せばよい。, を任意に取る。 を示せばよい。
連続写像 を と定める。
の連結性より,合成写像 は定数写像である。よって を得る。
連続写像 を と定める。
同様の議論で は定数写像であることが分かる。よって を得る。
こうして が示された。
連結性の伝播
この定理は後ほど使います。
の連結集合(連結な部分集合)の族 の共通部分 が空でない場合,和集合 は連結である。
3番の条件で得られる連続関数を張り合わせましょう。
連続関数 を考える。
任意に を取る。前の定理より を示せばよい。
各 について, を各 の制限した は, の連結性から定数写像である。
, となる を取り, を任意に取る。
上述したことから となる。よって となり定理が示された。
連結集合の閉包の連結性
連結集合の閉包は連結集合になります。次の定理を証明しましょう。
が連結ではないと仮定して矛盾を導く。
このとき, の開集合 であって となる。
であるため,上の式を に制限することで である。
であるため, を取ることができる。 とすると より である。これは と矛盾する。よって である。
同様に が従うが,これらは の連結性と矛盾する。こうして は連結である。
とおくことで連結集合の閉包が連結集合であることが分かります。
について開区間 と閉区間 は連結である。
実際, により連続写像 を定めると,これは同相写像を与えるため, の連結性から は連結である。
より も連結である。
弧状連結空間の性質
弧状連結空間の性質
簡単な性質
次に弧状連結空間の性質を紹介します。連結空間と似た性質が成り立ちます。
弧状連結空間の像
連結性同様に弧状連結性も連続写像で保たれます。
を弧状連結空間, を位相空間として を連続写像とする。
このとき は弧状連結空間である。
を任意の2点とする。
このとき が存在して , となる。
の弧状連結性より,, を満たす道 が存在する。
ここで連続写像 は を満たす道であるため は弧状連結であることが分かる。
弧状連結空間の積
弧状連結空間の積も弧状連結になります。
を連結空間とする。このとき は弧状連結空間である。
を任意に取る。
このとき, の弧状連結性から と を結ぶ道 と と を結ぶ道 を取ることができる。
ここで を と定めると,合成写像 は と を結ぶ道である。
弧状連結性の伝播
この性質も弧状連結空間で成立します。
の連結集合(連結な部分集合)の族 の共通部分 が空でない場合,和集合 は連結である。
3番の条件で得られる連続関数を張り合わせましょう。
を任意に取る。このとき が存在して となる。
を任意に取る。このとき の弧状連結性より となる道 と を結ぶ道 が存在する。
このとき,連続写像 を と定めると,これは と を結ぶ道になる。よって弧状連結性が示された。
弧状連結であれば連結
弧状連結であれば連結
弧状連結空間と連結空間で同じ性質が成り立つところをいくつか見てきました。実は弧状連結空間は常に連結空間になります。証明してみましょう。
弧状連結空間は連結空間になる。
位相空間 を弧状連結空間とする。
を固定する。
に対して と を結ぶ道を とおく。 とおく。前述した例より は連結である。さらに連結性は連続写像で保たれるため は連結空間である。
であるため である。一方 より上記の等号が成立する。
他方 である。
- 各 に対して は連結
であるため,前述の定理(連結性の伝播)から は連結空間である。
連結であるが弧状連結ではない例
連結であるが弧状連結ではない例
逆に連結空間は弧状連結になるのでしょうか? 実はそうとは限りません。
簡単な例
を と定める。(位相構造は の相対位相)
この位相空間は連結ではあるが,弧状連結ではない。
グラフで示すと次のようになります。この曲線は位相幾何学者の正弦曲線と呼ばれることがあります。
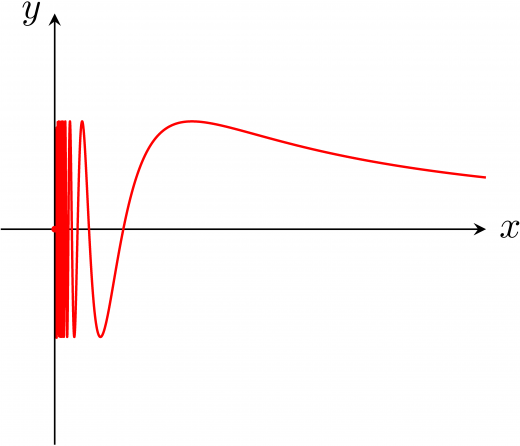
から原点を除いた部分集合を を とおく。 は連結である。
は の相対位相が定められているため, の開集合は, の開集合 を用いて と表されることに注意する。
弧状連結ではないこと
と を結ぶ道が無いことを示す。そのような道 があると仮定する。 とする。 側から順番に見て(はじめての)山頂と谷底を通る時を とする。つまり, であり。 なので, は定まらない。一方,道の連続性より となるはずであり,矛盾。
連結であること
が連結ではない,つまり , となるように開集合 を取ることができると仮定する。
として考えてよい。十分大きい正の整数 を取ると となる。よって, であり,これらはどちらも の開部分集合となる。
また,条件から となるが,これは の連結性と反する。
よって, は連結である。
連結性を用いた非同相の証明
連結性を用いた非同相の証明
連結性を用いて同相にはならないことの証明をしてみましょう。
の区間 と円周 は同相ではない。
と が同相であると仮定する。
同相写像を とおく。
ここで から を取り除いた集合を考える。
での像を考えることで誘導される同相写像 を考えることができる。
は同相であったため, は から1点除いた空間になる。これは連結空間になる。一方, は連結ではない。
連結性は同相で保たれるため,上記は が同相であることと矛盾する。よって と は同相ではない。
定義だけを見ると弧状連結のほうが連結っぽさがありますが,2点集合への連続写像の性質を想うと,連結空間が「過不足なく」連結であることが分かりますね。











