留数定理を用いたバーゼル問題の美しい証明

$\dfrac{1}{x^2-1}$ をマクローリン展開する。

$$\dfrac{1}{x^2-1} = - \sum_{k=0}^{\infty} x^{2k}$$

よって $$\dfrac{\log x}{x^2-1} = -\sum_{k=0}^{\infty} x^{2k} \log x$$ である。

これより $$\int_0^1 \dfrac{\log x}{x^2 - 1} dx = - \int_0^1 \sum_{k=0}^{\infty} x^{2k} \log x dx$$ となる。ここで単調収束定理（詳しくは ルベーグの収束定理 を参照）を用いると，積分と極限が交換でき $$\int_0^1 \dfrac{\log x}{x^2 - 1} dx = - \sum_{k=0}^{\infty} \int_0^1 x^{2k} \log x dx$$ となる。

項別積分すると $$\begin{aligned} &\int_0^1 x^{2k} \log x \\ &= \Big[ \dfrac{1}{2k+1} x^{2k+1} \log x \Big]_0^1\\ &\quad - \dfrac{1}{2k+1} \int_0^1 x^{2k+1} \cdot \dfrac{1}{x} dx\\ &= -\dfrac{1}{(2k+1)^2} \Big[ x^{2k+2} \Big]_0^1\\ &= - \dfrac{1}{(2k+1)^2} \end{aligned}$$ となる。

よって $$\int_0^1 \dfrac{\log x}{x^2-1} dx = \sum_{k=0}^{\infty} \dfrac{1}{(2k+1)^2}$$ を得る。

もとめる積分を $I$ とおく。

まず与式を $x = \dfrac{1}{y}$ に置換する。 $$\begin{aligned} &\int_{\infty}^1 \dfrac{-\log x}{x^{-2}-1} \left( - \dfrac{dx}{x^2} \right)\\ &= \int_1^{\infty} \dfrac{\log x}{x^2-1} dx \end{aligned}$$

よって $$2I = \int_0^{\infty} \dfrac{\log x}{x^2-1} dx$$ となる。

この積分を留数定理で計算する。

そのまま計算するのではなく $$\oint_{C} \dfrac{(\log z)^2}{z^2-1} dz$$ を考える。

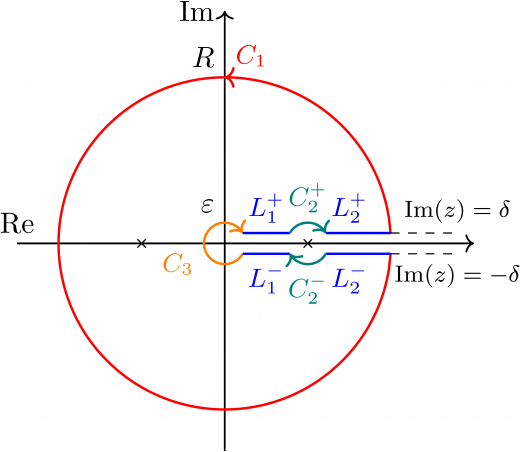
なお，下図のような積分路 $C$ を考える。

• $C_1$：半径 $R$，中心 $0$ の円のうち，$\mathrm{Re} (z) > 0 , \ -\delta < \mathrm{Im} (z) < \delta$ の部分を取り除いたもの
• $C_2^+$：半径 $\varepsilon$，中心 $0$ の円のうち，$\mathrm{Im} (z) > \delta$ の部分
• $C_2^-$：半径 $\varepsilon$，中心 $0$ の円のうち，$\mathrm{Im} (z) < -\delta$ の部分
• $C_3$：半径 $\varepsilon$，中心 $0$ の円のうち，$\mathrm{Re} (z) > 0 , \ -\delta < \mathrm{Im} (z) < \delta$ の部分を取り除いたもの
• $L_1^+$：$C_2^+$ と $C_3$ を結ぶ線分
• $L_1^-$：$C_2^-$ と $C_3$ を結ぶ線分
• $L_2^+$：$C_2^+$ と $C_1$ を結ぶ線分
• $L_2^+$：$C_2^-$ と $C_1$ を結ぶ線分

（$L_1^+,L_1^-,L_2^+,L_2^-$ は虚部が $\delta$ であることに注意）

留数定理より $$\begin{aligned} &\oint_{C} \dfrac{(\log z)^2}{z^2-1} dz\\ &= 2\pi i \; \mathrm{Res} \left( \dfrac{(\log z)^2}{z^2-1} , -1 \right)\\ &= 2\pi i \lim_{z \to -1} \dfrac{(\log z)^2}{z-1}\\ &= -\pi i (\log (-1))^2\\ &= -\pi i (\pi i)^2\\ &= \pi^3 i \end{aligned}$$ である。

$C_1$ 上での積分を評価する。

$$\begin{aligned} \lim_{R \to \infty} \left| \int_{C_1} \dfrac{(\log z)^2}{z^2-1} \right| & \leqq \lim_{R \to \infty} \int_{C_1} \dfrac{|\log z|^2}{|z|^2-1} |dz|\\ & \leqq \lim_{R \to \infty} \int_0^{2\pi} \dfrac{R(\log R)^2 + R\theta^2}{R^2-1} d\theta\\ &= \lim_{R \to \infty} \left( \dfrac{2 \pi R (\log R)^2}{R^2-1} + \dfrac{8\pi^3 R}{3(R^2-1)} \right)\\ &= 0 \end{aligned}$$ である。

$z = Re^{i\theta}$ と置換している。途中で $$\begin{aligned} |\log z|^2 &= |\log R + i\theta|^2\\ &\leqq (\log R)^2 + \theta^2 \end{aligned}$$ と計算している。

なお $\theta$ での積分の範囲は $[0,2\pi]$ ではないが，$[0,2\pi]$ に含まれるため，上記のような不等式で評価してよい。

$\;$

次に $C_3$ 上での積分を評価する。$\dfrac{1}{z^2-1}$ は $C_3$ 上で正則であるため，最大値 $M$ を持つことを用いる。 $$\begin{aligned} \lim_{\varepsilon \to 0} \left| \int_{C_3} \dfrac{(\log z)^2}{z^2-1} dz \right| &\leqq \lim_{\varepsilon \to 0} \int_{C_3} \dfrac{|\log z|^2}{|z^2-1|}|dz|\\ &\leqq \lim_{\varepsilon \to 0} \int_0^{2 \pi} M\varepsilon ((\log \varepsilon)^2 + \theta^2) d\theta\\ &= 0 \end{aligned}$$ である。

$\log z$ は $z = 1$ 近傍でローラン展開することで $$\log (z) = (z-1) + \dfrac{1}{2} (z-1)^2 + \cdots$$ と表される

$\;$

$C_2^+$ の計算

$z = \varepsilon e^{i\theta} + 1$ と置換する。このとき，ローラン展開により $$\log (z) = \varepsilon e^{i\theta} + \dfrac{1}{2} \varepsilon^2 e^{2i\theta} + \cdots$$ と表される。一方，十分小さい $\varepsilon$ において $$\dfrac{1}{z^2-1} = \dfrac{1}{\varepsilon e^{i\theta} (\varepsilon e^{i\theta} + 2)} \sim \dfrac{1}{2\varepsilon e^{i\theta}}$$ と表される。（これらの差分は $\varepsilon \to 0$ で $0$ に収束する）

よって，十分小さい $\varepsilon$ において $$\begin{aligned} \dfrac{(\log z)^2}{z^2-1} &\sim \dfrac{\varepsilon e^{i\theta}}{2\varepsilon e^{i\theta}} + O(\varepsilon^2)\\ &= \dfrac{\varepsilon e^{i\theta}}{2} + O(\varepsilon) \end{aligned}$$ と表される。

こうして $$\begin{aligned} &\lim_{\delta \to 0} \lim_{\varepsilon \to 0} \int_{C_2^+} \dfrac{(\log z)^2}{z^2+1} dz \\ &\to \lim_{\varepsilon \to 0} \int_{\pi}^{0} \left( \dfrac{\varepsilon e^{i\theta}}{2} + O(\varepsilon) \right) \varepsilon ie^{i\theta} d\theta \\ &= \lim_{\varepsilon \to 0} \varepsilon \times (\varepsilon \ \text{の整式}) = 0 \end{aligned}$$ となる。

$\:$

$C_2^-$ の計算

同様に置換をする。

前のケースとは異なり，偏角 $2\pi$ 分 $\log$ の値がずれて $$\log z = \log (1+\varepsilon e^{i\theta}) + 2\pi i$$ と表される。よって $$\begin{aligned} (\log z)^2 \sim (2\pi i)^2 + 4 \pi i \varepsilon e^{i\theta} + O(\varepsilon^2) \end{aligned}$$ となる。ゆえに $$\begin{aligned} \dfrac{(\log z)^2}{z^2-1} &\sim \dfrac{-4\pi^2 + 4\pi i \varepsilon e^{i\theta}}{2\varepsilon e^{i\theta}} + O(\varepsilon)\\ &= -\dfrac{2\pi^2}{\varepsilon e^{i\theta}} + 2\pi i + O (\varepsilon) \end{aligned}$$ と表される。

こうして $$\begin{aligned} &\lim_{\delta \to 0} \lim_{\varepsilon \to 0} \int_{C_2^-} \dfrac{(\log z)^2}{z^2+1} dz \\ &= \lim_{\varepsilon \to 0} \int_{\pi}^{2\pi} \left( -\dfrac{2\pi^2}{\varepsilon e^{i\theta}} + 2\pi i + O (\varepsilon) \right) \varepsilon ie^{i\theta} d\theta\\ &= \lim_{\varepsilon \to 0} \int_{\pi}^{2\pi} (-2\pi i+ O(\varepsilon)) d\theta\\ &= -2\pi^3 i \end{aligned}$$

以下，$L^+ = L_1^+ \cup L_2^+$，$L^- = L_1^- \cup L_2^-$ とする。

$L^{+},L^{-}$ 上での積分を評価する。

$L^+$ 上で被積分関数は $\dfrac{(\log (x+i\delta))^2}{(x+i\delta)^2-1}$ となる。有界区間（今は $[\varepsilon , R]$ 上を考える）これは $\delta \to 0$ で $\dfrac{(\log x)^2}{x^2-1}$ に一様収束する。

よって $$\begin{aligned} &\lim_{\delta \to 0} \int_{L^+} \dfrac{(\log z)^2}{z^2-1} dz =\\ &\int_{\varepsilon}^{1-\varepsilon'} \dfrac{(\log x)^2}{x^2-1} dx + \int_{1+\varepsilon'}^R \dfrac{(\log x)^2}{x^2-1} dx \end{aligned}$$ が得られる。（ただし $\varepsilon'$ は $\varepsilon \to 0$ で $0$ に収束する十分小さい正数）

同様に $L^-$ で被積分関数は $\dfrac{(\log (x-i\delta))^2}{(x+i\delta)^2-1}$ となり，$\delta \to 0$ で $\dfrac{(\log x + 2\pi i)^2}{x^2-1}$ に一様収束する。なお，$\log z = \log |z| + i \arg z$ であったことから，$L^-$ において $\arg z \to 2\pi$ であることに注意する。

こうして $$\begin{aligned} &\lim_{\delta \to 0} \int_{L^-} \dfrac{(\log z)^2}{z^2-1} dz \\ &= \int_{R}^{1+\varepsilon'} \dfrac{(\log x + 2\pi i)^2}{x^2-1} dx + \int_{1-\varepsilon'}^{\varepsilon} \dfrac{(\log x + 2\pi i)^2}{x^2-1} dx\\ &= -\int_{\varepsilon}^{1-\varepsilon'} \dfrac{(\log x + 2\pi i)^2}{x^2-1} dx-\int_{1+\varepsilon'}^R \dfrac{(\log x + 2\pi i)^2}{x^2-1} dx \end{aligned}$$ が得られる。

以上をまとめると $$\begin{aligned} &\lim_{R \to \infty} \lim_{\varepsilon \to 0} \lim_{\delta \to 0} \oint_C \dfrac{(\log z)^2}{z^2-1} dz\\ &= \int_{0}^{\infty} \dfrac{(\log x)^2}{x^2-1} dx -\int_{0}^{\infty} \dfrac{(\log x + 2\pi i)^2}{x^2-1} dx\\ &= \int_{0}^{\infty} \dfrac{4\pi^2-4\pi i \log x}{x^2-1} dx\\ &= 4\pi^2\int_{0}^{\infty} \dfrac{1}{x^2-1} dx-4 i \pi \int_{0}^{\infty} \dfrac{\log x}{x^2-1} dx \end{aligned}$$ となる。一方で $$\begin{aligned} &\lim_{R \to \infty} \lim_{\varepsilon \to 0} \lim_{\delta \to 0} \oint_C \dfrac{(\log z)^2}{z^2-1} dz\\ &=\pi^3 i-2\pi^3 i \\ &= -\pi^3 i \end{aligned}$$ である。

虚部を比較することで $$I = \dfrac{1}{2} \int_{0}^{\infty} \dfrac{\log x}{x^2-1} dx = \dfrac{\pi^2}{8}$$ が得られる。