定常分布・極限分布・詳細釣り合い条件・収束定理

この記事では，マルコフ連鎖について考えます。

マルコフ連鎖の基本は マルコフ連鎖の基本とコルモゴロフ方程式 で解説しています。

以下では，例として「晴れ、曇、雨」という3つの状態を持つ以下のようなマルコフ連鎖を考えます。 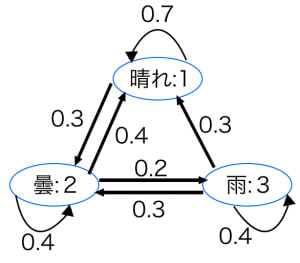※実際の天気はマルコフ連鎖ではないですが，簡単のため「明日の天気は今日の天気のみで決まる」状況を想定します。推移確率行列は $$P=\begin{pmatrix} 0.7 &0.3& 0\\0.4 & 0.4 & 0.2\\ 0.3 & 0.3 & 0.4\end{pmatrix}$$ です。

$\overrightarrow{\pi}$ は横ベクトルで確率ベクトル（つまり各成分が $0$ 以上で和が $1$ になるベクトル）です。

定常分布の意味

• 確率ベクトル $\overrightarrow{x}$ に対して，その1時刻後の確率分布は $\overrightarrow{x}P$ になります。
• つまり，定常分布とは「現在の確率分布」と「1時刻後の確率分布」が同じになる分布です。
• 一度その分布になったらずっとその分布のままであるものとも言えます。

例

さきほどの例$$P=\begin{pmatrix} 0.7 &0.3& 0\\0.4 & 0.4 & 0.2\\ 0.3 & 0.3 & 0.4\end{pmatrix}$$

において $\overrightarrow{\pi}=\left(\dfrac{5}{9},\dfrac{3}{9},\dfrac{1}{9}\right)$ とおくと $\overrightarrow{\pi} P=\overrightarrow{\pi}$ となるので $\overrightarrow{\pi}$ は定常分布です。

以下，状態空間のサイズを $n$ とし，確率ベクトル $\overrightarrow{\pi}$ の第 $i$ 成分を $\pi_i$，推移確率行列 $P$ の $ij$ 成分を $p_{ij}$ と書きます。

この $$\pi_ip_{ij}=\pi_jp_{ji}$$ という式を詳細釣り合い条件と言います。

※詳細釣り合い条件を満たすなら定常分布ですが，逆は成立しません。つまり，定常分布でも詳細釣り合い条件を満たさない場合もあります。

極限分布の意味

極限分布は「どんな分布からスタートしても時間が十分経過すればそこにたどり着くような確率分布」です。

定常分布との関係

• 極限分布は定常分布です。

• 一方，定常分布が極限分布とは限りません。しかし，後述の収束定理にあるように，ある条件を満たすときには定常分布が極限分布になります。

「既約」「非周期的」の意味

• マルコフ連鎖が既約とは，「すべての状態からすべての状態に到達しうる」ことを表します。つまり，任意の $i,j$ に対して「$P^n$ の $ij$ 成分が $0$ でない $n$ が存在する」ことを表します。

• マルコフ連鎖の状態 $s$ の周期とは，「$s$ からスタートして $s$ に戻ってくるのが $T$ の倍数に限る」という条件を満たす最小の $T$ のことです。

• マルコフ連鎖が非周期的とは，全ての状態の周期が $1$ であることを表します。

例

さきほどの天気の例は「既約」で「非周期的」です。 さらに，定常分布 $\overrightarrow{\pi}=\left(\dfrac{5}{9},\dfrac{3}{9},\dfrac{1}{9}\right)$ が存在しました。よって，収束定理より $\overrightarrow{\pi}=\left(\dfrac{5}{9},\dfrac{3}{9},\dfrac{1}{9}\right)$ が極限分布になります。スタートがどんな分布でも（例えば今日が晴れでも曇でも雨でも）十分先の予測は「晴れの確率 $\dfrac{5}{9}$，曇の確率 $\dfrac{3}{9}$，雨の確率 $\dfrac{1}{9}$」に近づきます。

なお，収束定理の証明は，参考文献：確率数理工学補足資料 マルコフ連鎖 をどうぞ。